3.1. Явление поглощения оптического излучения в атмосфере
Атмосферу принято рассматривать как среду, состоящую из смеси газов, водяного пара, мельчайших взвешенных частиц, называемых аэрозолем. В атмосфере содержится [1, 10]:
N2 – 78% по объему;
Н2О – (~10-5% ¸ 4,5%) по объему;
СО2 – 0,03% по объему;
О3 – 2,7 · 10-6% по объему.
Кроме того, содержится O2, СО, СН4, Ne, H2, NO2, N2O и другие газовые компоненты.
Современные ОЭП и С работают в условиях, когда излучение наблюдаемых объектов поступает на входной зрачок оптической системы ослабленным и искаженным за счет влияния слоев атмосферы между объектами и ОЭП и С. Общее ослабление излучения в атмосфере обусловлено явлением поглощения газовыми компонентами, в результате которого происходит преобразование энергии излучателя в другие ее виды, а также явлением молекулярного и аэрозольного рассеяния, состоящим в изменении направленности излучения. В общем случае неоднородной среды, ослабление оптического излучения описывается законом Бугера – Ламберта – Бера [1]:
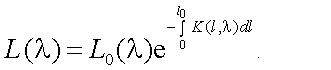 |
(3.1) |
Здесь, L(λ) – спектральная яркость излучения, прошедшего путь l0;
L0(λ) – спектральная яркость излучения до вхождения в среду;
К(l, λ) – спектральный показатель ослабления, который имеет размерность [км-1].
Формула (3.1) может быть записана в следующем виде:
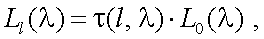 |
(3.2) |
где 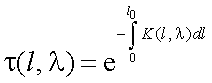 – коэффициент пропускания среды, или прозрачность неоднородного слоя толщиной l0 на длине волны λ.
– коэффициент пропускания среды, или прозрачность неоднородного слоя толщиной l0 на длине волны λ.
Если слой l0 однороден, то спектральный коэффициент прозрачности τ(l, λ) определяется следующим образом (так как в этом случае К(l, λ) = К(λ) = const):
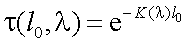 . . |
(3.3) |
Показатель ослабления К(l, λ) является суммой показателей рассеяния σ(l, λ) и поглощения α(l, λ):
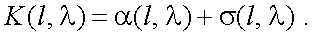 |
(3.4) |
3.2. Явление рассеяния в атмосфере
Молекулярное рассеяние. Данный вид рассеяния является следствием возникновения неоднородностей плотности воздуха, вызванных флуктуациями этой величины. Спектральный показатель молекулярного рассеяния определяется по следующей формуле:
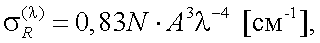 |
(3.5) |
где N – число молекул в 1 см3;
А – площадь поперечного сечения молекулы (см2);
λ – длина волны излучения (см).
Аэрозольное рассеяние. Рассмотрим подробнее аэрозольное рассеяние и ослабление. Рассеяние на отдельных частицах характеризуется показателем рассеяния σ, для характеристики рассеивающих свойств частицы по направлениям используется понятие угловой функции рассеяния, которую часто называют индикатрисой рассеяния:
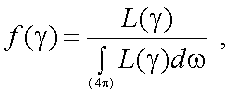 |
(3.6) |
где L(γ) – интенсивность излучения, рассеянного частицей в направлении угла γ;
dω – элементарный телесный угол.
Если в определенном единичном объеме рассеивающей среды находится N частиц, распределение по размерам которых описывается функцией f(r), то объемный показатель аэрозольного рассеяния совокупности частиц N будет выражаться формулой:
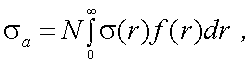 |
(3.7) |
здесь, σ(r) – объемный показатель аэрозольного рассеяния i-й частицы радиуса r. В теории рассеяния частиц сферической формы, разработанной Ми [10], рассмотрены вопросы рассеяния на частицах произвольных размеров и получены выражения для σR и σа в виде функций параметра Ми ρ = 2πr/λ. Для объемного показателя поглощения αа совокупности частиц N можно получить выражение, аналогичное (3.7):
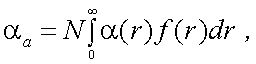 |
(3.8) |
где α(r) – показатель поглощения i-й частицы радиуса r. Тогда, с использованием формулы (3.7) и (3.8), объемный показатель ослабления объема N частиц будет иметь вид:
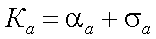 . . |
(3.9) |
3.3. Поглощение излучения газами атмосферы
Перейдем теперь к явлению поглощения излучения газовыми компонентами атмосферы. Выбор спектральных диапазонов, удобных для работы ОЭП в видимой и ИК областях спектра, в основном основывается на учете полос пропускания атмосферы. Анализ коэффициента поглощения излучения данной длины волны или частоты того или иного газа в атмосфере ведется на основе моделей полос поглощения. Как показали специальные исследования процессов, влияющих на ширину спектральных линий поглощения, в приземном слое атмосферы ширина линий обусловлена столкновением молекул. Теория данного процесса была разработана Лорентцем, который получил формулу распределения интенсивности спектральных линий поглощения как функции частоты υ. Для группы перекрывающихся линий (полосы) спектральный коэффициент поглощения равен
[10]:
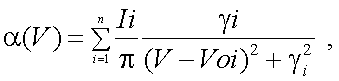 |
(3.10) |
где Ii – интегральная интенсивность i-й перекрывающейся линии;
γI – полуширина линии;
Voi – частота центра линии.
Вообще говоря, вычисления α(V) практически возможны, если известны модели полос поглощения. Современная атмосферная оптика оперирует моделями Эльзассера, Кинга, статистической моделью, квазистатистической и комбинированной моделями, с использованием которых проводятся расчеты α(V) мощных полос поглощения Н2О и СО2, а также других газов [10, 11]. Наиболее мощная поглощающая компонента атмосферы – Н2О имеет значительные полосы поглощения, располагающиеся около λ0 = 0,94; 1,1; 1,38; 1,87; 2,7; 3,2 и 6,3 мкм. Наличие этих полос вызвано колебательно-вращательным движением молекул воды. Молекулы СО2 создают значительное поглощение около λ0 = 1,4; 1,6; 2,0; 4,3; 4,8; 5,2; 9,4; 10,4 и 13,9 мкм, а молекулы О3 ослабляют излучение около λ0 = 9,6 мкм. Для расчетов параметров ОЭП и С очень важно отметить наличие «окон» пропускания атмосферы. Так, в атмосфере приземного слоя имеются следующие полосы пропускания: Δλ = 0,95 – 1,05; 1,2 – 1,3; 1,5 – 1,8; 2,1 – 2,4; 3,3 – 4,2; 4,5 – 5,0; 8 – 13 мкм. Исходя из исследуемых диапазонов длин волн окон прозрачности атмосферы, целесообразно выбирать и рабочие области спектра оптико-электронных приборов. Помимо чисто расчетных методов определения функций пропускания атмосферы [10, 11], в литературе имеется ряд эмпирических формул, которые удобны своей простотой. Так, Эльдер и Стронг предложили следующую формулу для функции пропускания τ горизонтальными трассами:
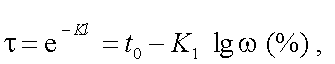 |
(3.11) |
где t0 и К1 – параметры, которые зависят от λ;
ω = Vl – слой осажденной воды в мм; (l – путь излучения в км; V – абсолютная влажность, которая практически равна количеству осажденной воды на трассе 1 км).
Для определения V необходимо умножить величину относительной влажности на количество осажденной воды. Формула (3.11) справедлива для трасс, расположенных на высотах
Н = 2 ÷ 3 км. Для высот Н > 3 км, по методике Эльдера и Стронга, величина ω имеет вид [12]:
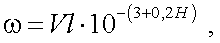 |
(3.12) |
где Н измеряется в километрах.
Ученые ИОА СО РАН под руководством В.Е. Зуева получили аппроксимационную формулу для интегральной прозрачности τ в диапазоне 0,7 – 14 мкм [10]:
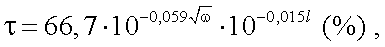 |
(3.13) |
где ω – осажденный слой воды в см;
l – дистанция в км.
3.4. Флуктуации параметров оптического излучения при распространении в атмосфере
При распространении оптического излучения в атмосфере наблюдаются флуктуации его параметров: интенсивности, фазы, состояния поляризации, угла прихода, т.е. расходимости и т.д. Эти флуктуации обусловлены турбулентными явлениями, связанными с колебаниями плотности воздуха, т.е. его показателя преломления.
1. Флуктуации интенсивности приходящего оптического излучения (эффект «мерцания»).
Мерой флуктуации интенсивности служит дисперсия флуктуации lg силы излучения источника
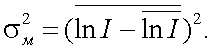 |
(3.14) |
Допустим, что длина трассы l намного больше внешнего масштаба lВ турбулентности. Тогда плотность распределения вероятности Р(I) амплитуды оптического сигнала имеет вид:
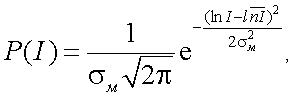 |
(3.15) |
т. е. подчиняется логарифмически-нормальному закону статистики, причем величина дисперсии σ2м равна:
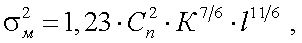 |
(3.16) |
где К = 2π/λ, а Сп – структурная постоянная турбулентности показателя преломления, величина, которая зависит от времени суток, метеорологической дальности видимости SМ и высоты Н. При этом должно выполнятся условие:
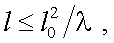 |
(3.17) |
где lо – внутренний масштаб турбулентности. Мерцание имеет низкочастотный временной характер, а максимум этого спектра лежит на частоте
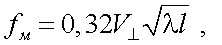 |
(3.18) |
где 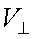 – скорость ветра перпендикулярна направлению излучения.
– скорость ветра перпендикулярна направлению излучения.
С увеличением зенитного угла Z наблюдаемого источника излучения амплитуда мерцания возрастает по закону sec Z, а частота уменьшается. Так у горизонта fм ≈ 5 – 10 Гц, а вблизи зенита fм ~ 1 000 Гц.
2. Флуктуация фазы и угла прихода излучения.
Изменения хода лучей из-за турбулентности атмосферы приводят к флуктуации фазы вдоль и поперек пучка. Поперечные флуктуации нарушают пространственную когерентность волнового фронта, искривляют и изгибают пучок, вызывают «дрожание» изображения. Флуктуации фазы вдоль пучка уменьшают временную когерентность. Выяснено, что выражение для структурной функции фазы φ имеет вид:
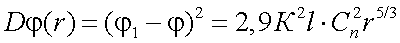 |
(3.19) |
при 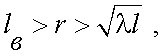
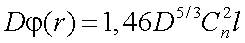 |
(3.20) |
при 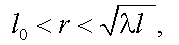 а дисперсия угла прихода излучения для ОЭП с входным зрачком D, определяется как
а дисперсия угла прихода излучения для ОЭП с входным зрачком D, определяется как
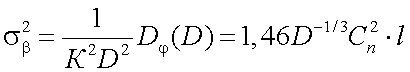 |
(3.21) |
при 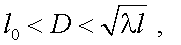
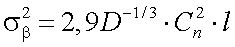 |
(3.22) |
при
 К = 2π/λ.
К = 2π/λ.
3. Рефракция.
Из-за рефракции оптический луч входит в зрачок приемной системы под углом αР:
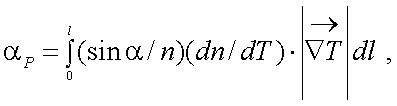 |
(3.23) |
где α – угол между направлением градиента
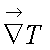 и осью ОЭП;
и осью ОЭП;
dn/dT – температурный градиент показателя преломления.

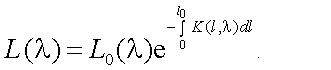
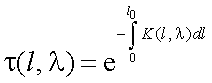 – коэффициент пропускания среды, или прозрачность неоднородного слоя толщиной l0 на длине волны λ.
– коэффициент пропускания среды, или прозрачность неоднородного слоя толщиной l0 на длине волны λ.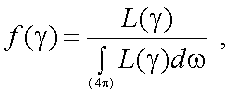
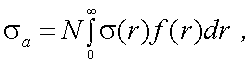
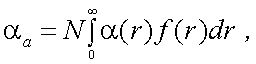
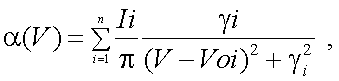
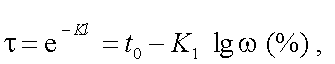
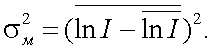
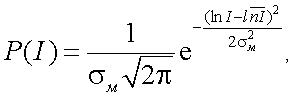
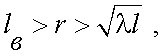
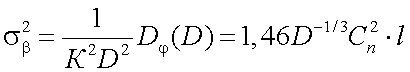
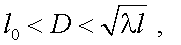
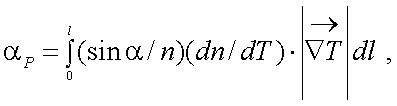
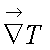 и осью ОЭП;
и осью ОЭП;