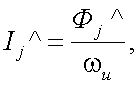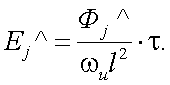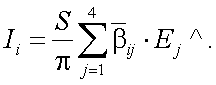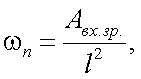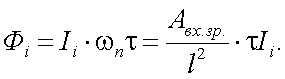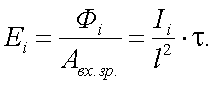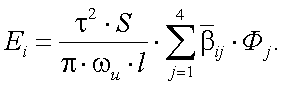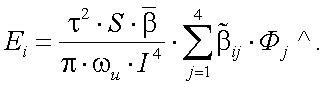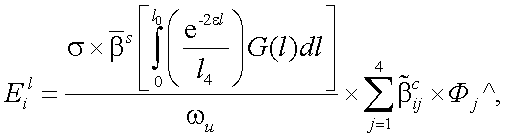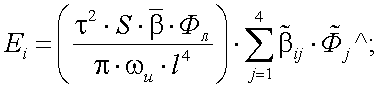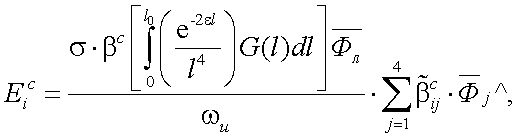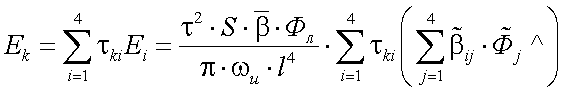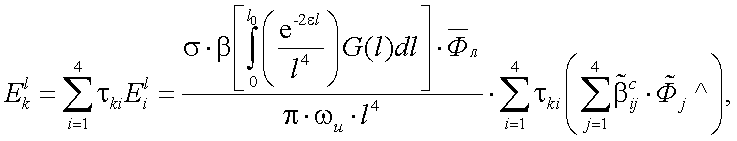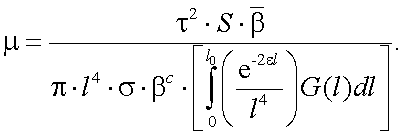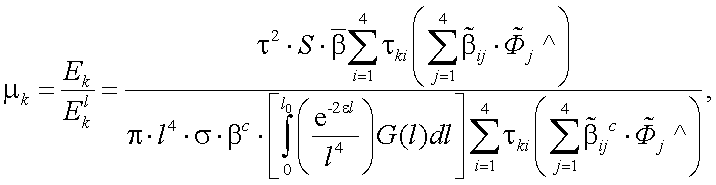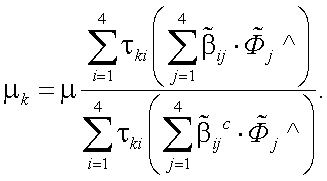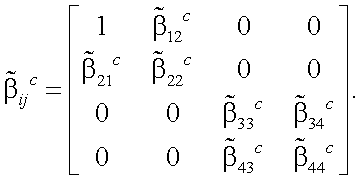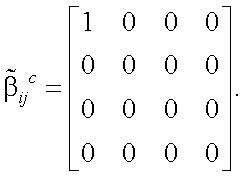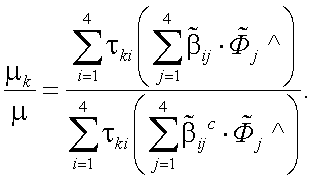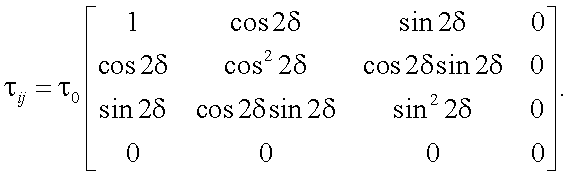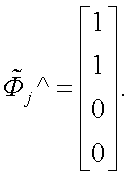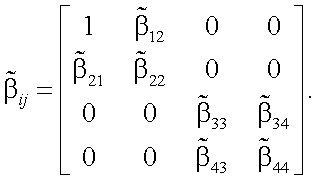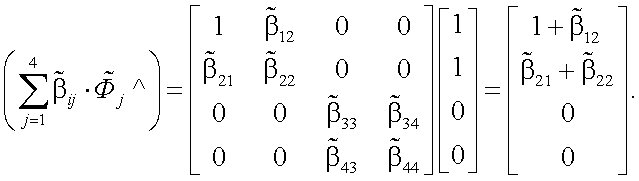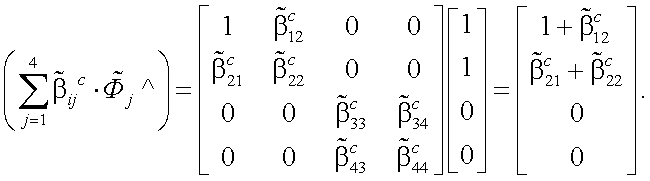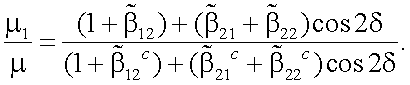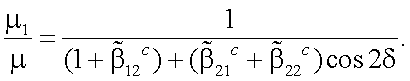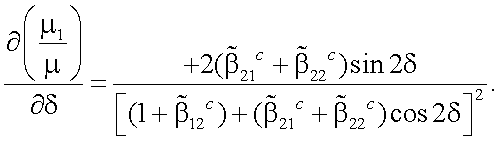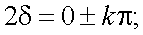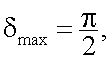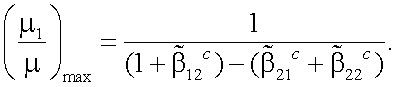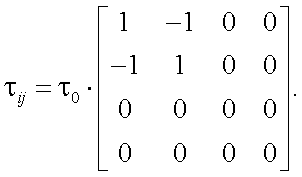Пусть Фjˆ – компоненты вектор-параметра Стокса мощности лазера передающей системы АОЭП. Тогда компоненты вектор-параметра Стокса силы излучения передающей системы будут следующие (рис. 13.1 и 13.2):
 |
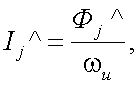(13.1) |
где ωи– телесный угол расходимости лучей лазера на выходе передающей системы АОЭП, j = 1, 2, 3, 4.
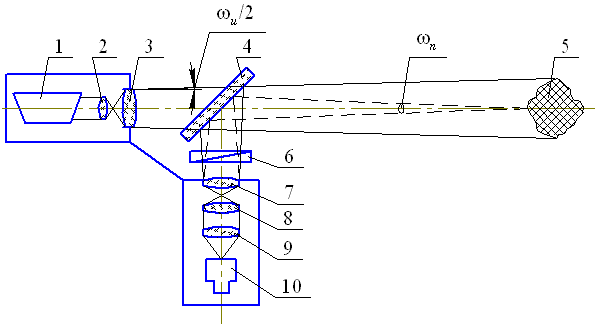
Рис. 13.1. Схема активного ОЭП (АОЭП) с поляризационной фильтрацией
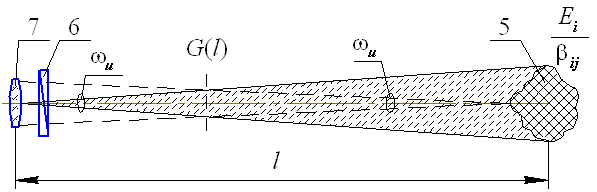
Рис. 13.2. Эквивалентная схема работы АОЭП с поляризационной фильтрацией
В месте расположения объекта на расстоянии l вектор-параметр Стокса Ijˆ создает энергетическую освещенность на объекте, компоненты вектор-параметр Стокса которого будут
 |
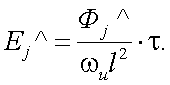(13.2) |
В связи с тем, что характеристикой объекта в поляризованном свете является матрица отражения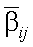 
, то при взаимодействии Ejˆ c 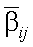формируются компоненты вектор-параметр Стокса отраженного излучения объекта; так компоненты вектор-параметр Стокса для энергетической яркости будут:
|
|
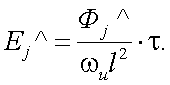(13.3) |
Если S – площадь объекта в направлении приемной части АОЭП, то для силы излучения объекта имеем:
 |
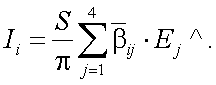(13.4) |
Так как приемная часть имеет апертурный угол ωп, который равен
 |
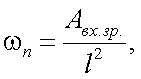(13.5) |
то поток Фi на входном зрачке АОЭП получит значение:
 |
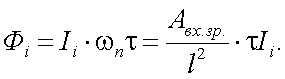(13.5') |
Тогда, учитывая (13.5'), компоненты вектор-параметра Стокса для энергетической освещенности на поверхности приемника системы, будут равны:
 |
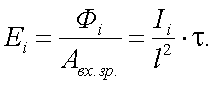(13.6) |
И, наконец, подставляя (13.4) с учетом (13.3) и (13.2) в (13.6), получаем следующее выражение для Ei:
 |
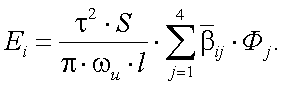(13.7) |
Учитывая, что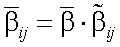 
, где 
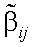– нормированная матрица яркости объекта, (13.7) принимает вид:
 |
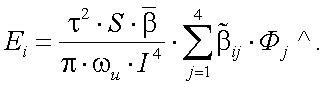(13.8) |
Аналогичным образом можно получить выражение, формирующее вектор-параметр Стокса энергетической освещенности рассеянного излучения слоя l:
 |
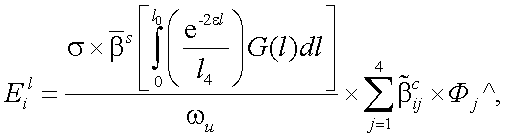(13.9) |
где G(l) – площадь, образуемая конусами излучения и визирования в плоскости перпендикулярной оси приемной системы прибора. Следует отметить, что рассеянное излучение слоя l между объектом и АОЭП представляет собой излучение диффузной помехи в АОЭП.
Выражение (13.8) и (13.9) можно еще представить в виде:
 |
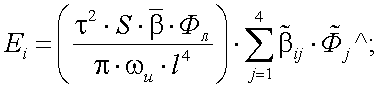(13.10) |
 |
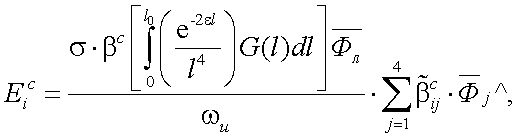(13.11) |
где Фл – мощность лазера;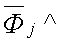 
– нормированный вектор Стокса лазера.
Если поместить перед входным объективом приемной системы АОЭП поляризационный фильтр, который имеет матрицу преобразования (пропускания) τki, то на выходе поляризационного фильтра получаем:
- для компонент вектор-параметра Стокса энергетической освещенности, создаваемой излучением объекта:
 |
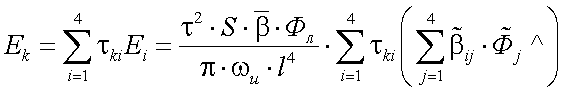(13.12) |
и излучением помехи
 |
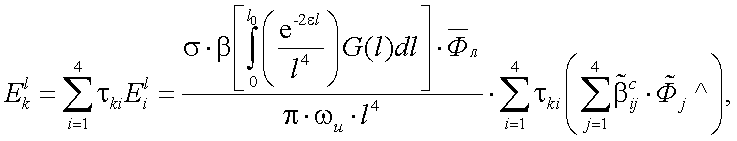(13.13) |
(k = 1, 2, 3, 4).
Для случая неполяризованного излучения отношение «сигнал/помеха» будет иметь вид:
 |
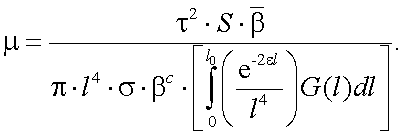(13.14) |
В случае поляризованного излучения отношение «сигнал/помеха» будет определяться отношением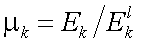 
:
 |
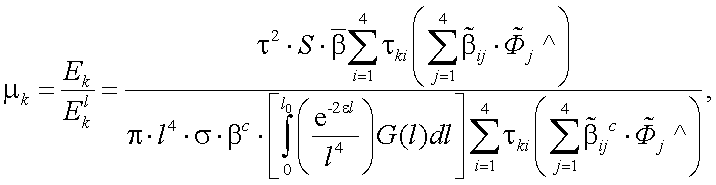(13.15) |
и, учитывая (13.14), (13.15) принимает вид:
 |
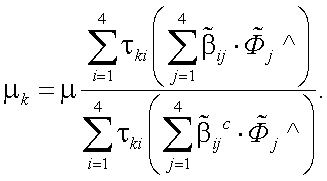(13.16) |
Сущность поляризационной фильтрации состоит в выборе такой матрицы τki, чтобы отношение «сигнал/помеха» в поляризованном свете при заданных конкретных значениях 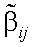и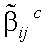 
было максимальным и превышало отношение «сигнал/помеха» в неполяризованном свете. Рассмотрим конкретный случай поляризационной фильтрации излучения диффузной помехи типа «дымка».
Согласно литературным данным, нормированная матрица рассеянного излучения дымки имеет вид [30]:
 |
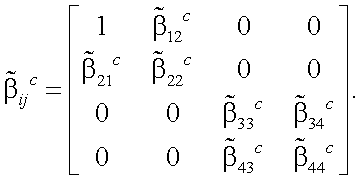(13.17) |
В свою очередь, нормированная матрица отражения диффузного объекта представляется в виде:
 |
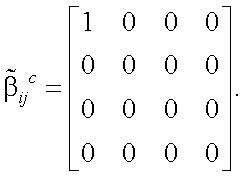(13.18) |
Выражение (13.16) запишем в виде:
 |
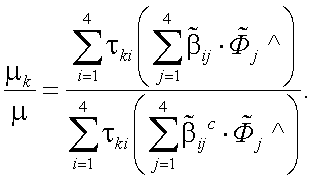(13.19) |
Из общих соображений известно, что матрица поляризационного фильтра имеет вид (для неизвестного значения угла δ):
 |
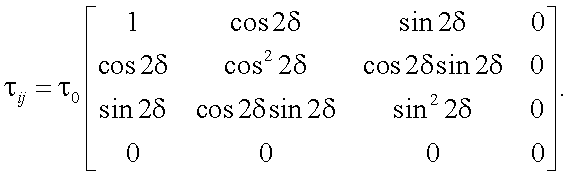(13.20) |
Необходимо определить значение δ, при котором (13.19) имеет максимум для условий (13.17) и (13.18) при освещении объекта светом, вектор-параметр Стокса нормированной мощности которого имеет вид:
 |
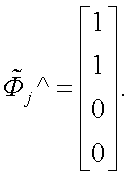(13.21) |
Решение осуществляется следующим образом. Определим сначала выражение в скобках формулы (13.19) в общем виде, т.е. когда 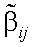имеет общий вид:
 |
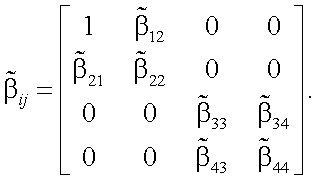(13.22) |
В числителе:
 |
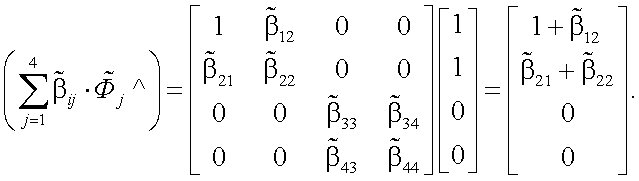(13.23) |
В знаменателе:
 |
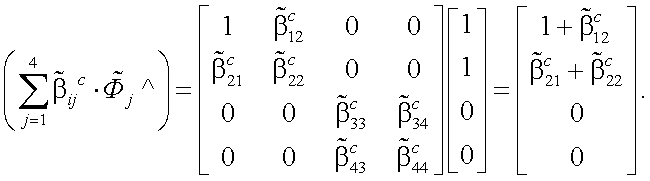(13.24) |
Подставим теперь (13.23) и (13.24) в (13.19) и напишем выражение для μk/μ с учетом (13.20) при k = 1:
 |
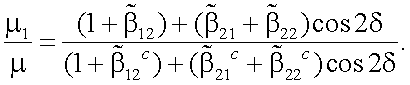(13.25) |
Так как объект отражает диффузно, то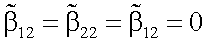 
и
 |
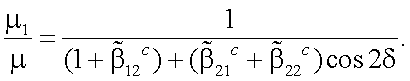(13.26) |
Найдем экстремум отношения μ1/μ, взяв производную по δ:
 |
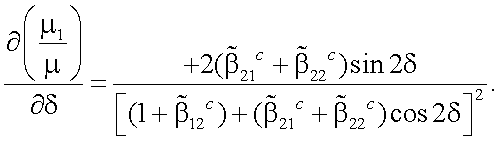(13.27) |
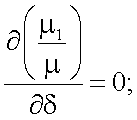
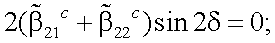
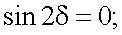
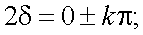
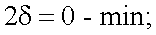
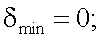
При k = 1, 2δ = π
 |
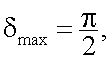(13.28) |
 |
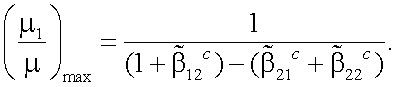(13.29) |
Теперь подставив (13.28) в (13.20), получим, что матрица оптического фильтра имеет вид:
 |
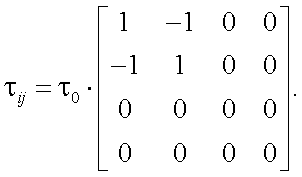(13.30) |
Таким образом, на основании (13.28) мы показали что матрица (13.30) подобрана оптимально с точки зрения максимизации отношения «сигнал/помеха».
