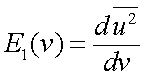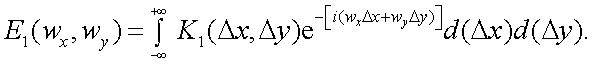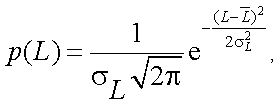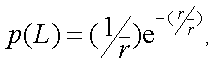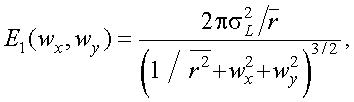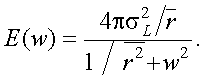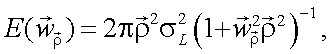4.1. Детерминированные сигналы и способы их описания
Сигналом принято называть физический процесс, несущий информацию и пригодный для передачи на расстояние [1]. В ОЭП и С носителем информации является оптическое излучение. Рассмотрим периодические сигналы, которые, как правило, содержат несущую информацию о наблюдаемых объектах в виде изменяющихся амплитуды, фазы и частоты.
1. Сложный периодический процесс.
Любой сложный периодический сигнал может быть представлен с помощью ряда Фурье в виде суммы элементарных гармонических колебаний. Пусть функция U(t), заданная в интервале от t1 до t2, повторяется с частотой ω1 = 2π/Т. Тогда, с несущественными математическими погрешностями, сводящимися к тому, что функция должна быть:
а) непрерывной или иметь конечное число разрывов;
б) также иметь в пределах одного периода конечное число max и min (условие Дирихле), функция U(t) может быть представлена рядом Фурье в виде суммы тригонометрических функций:
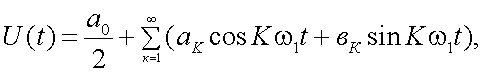 |
(4.1) |
где
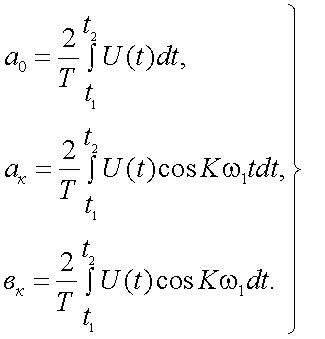 |
(4.2) |
Разложение сигнала U(t) может быть записано и в другой форме.
Пусть
 , , |
(4.3) |
т.е.
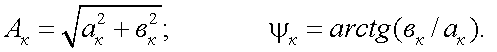
Тогда найдем, что
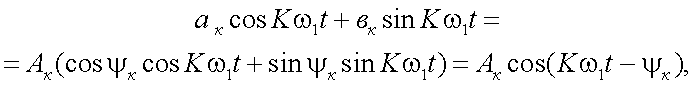
и
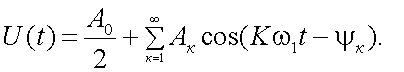 |
(4.4) |
где А0 = а0.
Следовательно, сигнал U(t) определяется совокупностью значений АК и ψК. Запишем теперь ряд Фурье в комплексной форме. Известно, что
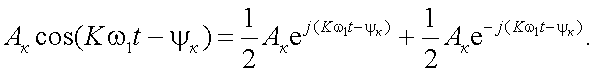
Тогда
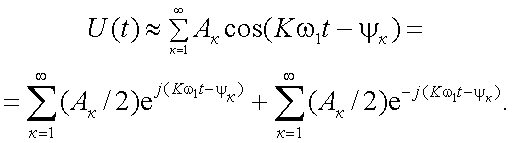 |
(4.5) |
Можно убедиться, что АК – четная функция относительно к, а ψК – функция нечетная. Это получается, используя (4.3) и (4.2), откуда имеем, что

и
 |
(4.6) |
Следовательно
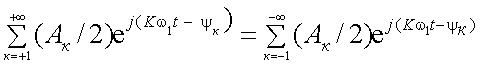
и
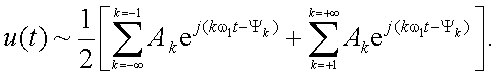
Кроме того, при k = 0 bк = b0 = 0;

то
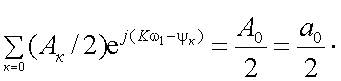 |
(4.7) |
Таким образом,
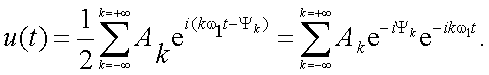 |
(4.8) |
Обозначая
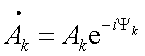 , , |
(4.9) |
найдем окончательное выражение сигнала u(t) в комплексной форме:
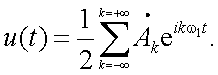 |
(4.10) |
2. Спектры непериодических сигналов.
Предположим, что сигнал задан в виде функции времени, удовлетворяющей условию Дирихле и абсолютно интегрируемой. Для удобства вывода примем, что u(t) действует в конечном интервале
t1 < t< t2, а в целях проведения гармонического анализа, превратим u(t) в периодическую u1(t) путем повторения ее с произвольным периодом
T > (t2 - t1). Тогда, для u1(t) ряд Фурье имеет вид:
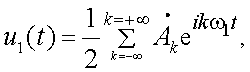 |
(4.11) |
причем амплитуда гармоник будет тем меньше, чем больше Т:
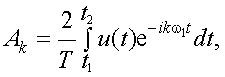 |
(4.12) |
а количество гармоник будет бесконечно большим, так как основная частота 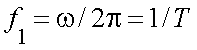 при T → ∞ стремится к 0, т. е. расстояние между спектральными линиями становится бесконечно малым, а спектр сплошным.
при T → ∞ стремится к 0, т. е. расстояние между спектральными линиями становится бесконечно малым, а спектр сплошным.
Действительно,
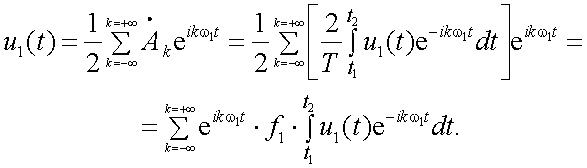 |
(4.13) |
При T → ∞ u1(t) = u(t) f1 = df kω1 = ω = 2πf , а операция суммирования превращается в операцию интегрирования, т.е.
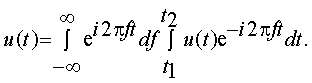 |
(4.14) |
Обозначим внутренний интеграл некоторой функцией частоты с волнистой линией сверху, показывающей, что при вычислении этой функции осуществляется разложение Фурье:
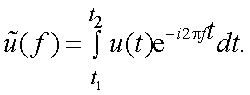 |
(4.15) |
Тогда найдем
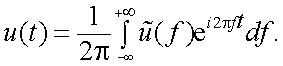 |
(4.16) |
Функция 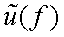 называется прямым преобразованием Фурье, а
называется прямым преобразованием Фурье, а 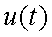 – обратным преобразованием Фурье.
– обратным преобразованием Фурье.
Достаточно часто функцию 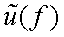 называют спектральной плотностью, спектральной характеристикой или комплексным спектром Фурье функции
называют спектральной плотностью, спектральной характеристикой или комплексным спектром Фурье функции 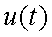 .
.
Преобразование Фурье, естественно, может быть приемлемо не только к функции времени, но и к функции u(x) пространственной координаты
x. В этом случае спектр Фурье
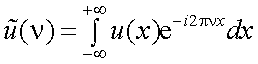 |
(4.17) |
или
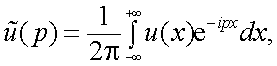 |
(4.18) |
где p = (2π/λ) круговая пространственная частота; ν = (1/λ) – линейная пространственная частота.
В этом случае 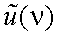 измеряется в [В·см],
измеряется в [В·см], 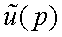 – в [В·рад-1], если амплитуду выражать в [В] , а x в [см].
– в [В·рад-1], если амплитуду выражать в [В] , а x в [см].
4.2. Свойства спектров сигналов. Свертка спектров сигналов
Основные свойства спектров определяются рядом теорем, которые рассмотрим применительно к пространственным координатам [2]:
А. Теорема о спектре суммы (свойство линейности).
Пусть функции u1(x) и u2(x) имеют спектры 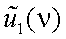 и
и 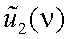 , т.е.
, т.е.
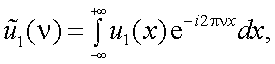
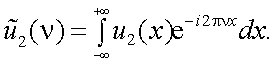
Тогда сумма спектров имеет вид:
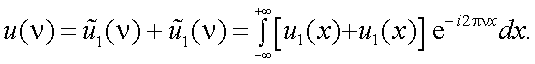
Б. Теорема запаздывания.
Пусть функция u(x) имеет спектр
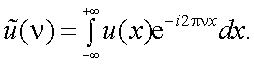
Требуется найти спектр 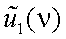 , соответствующий u1(x) = u(x-x0).
, соответствующий u1(x) = u(x-x0).
По определению имеем
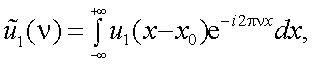
то, проведя замену переменной интегрирования на x1 = x-x0, получим
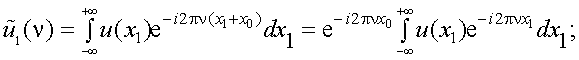
но
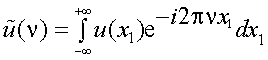
и
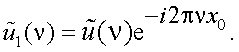 |
(4.19) |
В. Теорема смещения, или теорема о транспозиции (переносе) спектра.
Пусть спектр функции u(x) есть 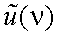 . Очевидно, что смещенный спектр
. Очевидно, что смещенный спектр
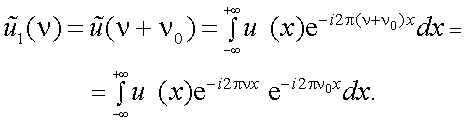
Обозначив 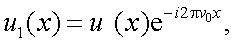 найдем
найдем
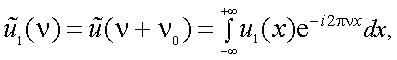
т.е. смещенным спектром обладает функция
 |
(4.20) |
Следовательно, функции u(x) соответствует спектр 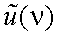 , а функции u1(x) – смещенный спектр
, а функции u1(x) – смещенный спектр 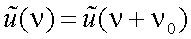 .
.
Г. Закон сохранения энергии (равенство Парсеваля) или теорема о связи между произведениями функций и их комплексных спектров.
Пусть заданы две функции u1(x) и u2(x). В соответствии с прямым преобразованием Фурье имеем:
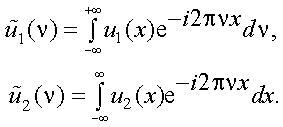
На основании обратного преобразования Фурье можно найти
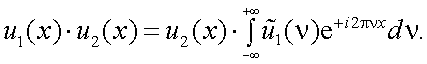 |
(4.21) |
Интегрируя (4.21) по x в пределах ± ∞, получим
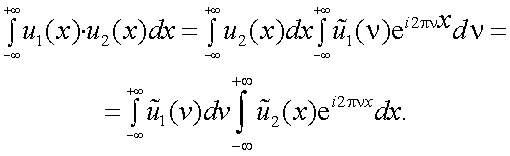 |
(4.22) |
Но внутренний интеграл представляет собой сопряженный спектр функции u2(x). Следовательно,
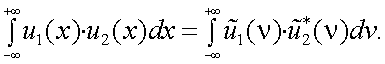 |
(4.23) |
Закон сохранения энергии W будет выражаться следующим образом.
Если, 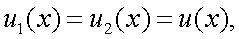 то
то 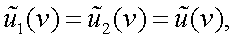 и
и 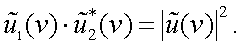
Тогда
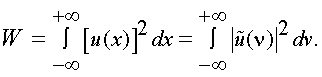 |
(4.24) |
Д. Теорема о свертке спектров.
Пусть задано две функции u1(x) и u3(x). Их комплексные спектры u1(m) и u3(m). Тогда можно записать следующее исходное равенство:
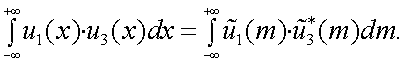 |
(4.25) |
Рассмотрим также функцию u2(x) со спектром u2(m), удовлетворяющую соотношению:
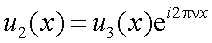 ,
,
или
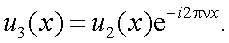
Тогда в соответствии с теоремой смещения спектр функции u1(x) равен смещенному спектру u2(x), т. е.
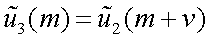
или
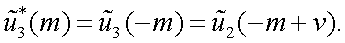
Тогда можно преобразовать левую и правую части уравнения (4.25).
1. Левая часть:
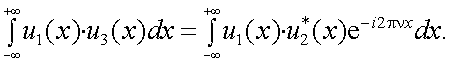 |
(4.26) |
Полученное выражение (4.26) представляет собой спектр произведения двух функций, и обозначим его 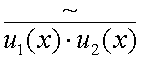 .
.
2. Правая часть:
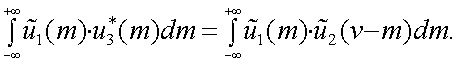 |
(4.27) |
Выражение (4.27) представляет собой операцию интегрирования, которую принято называть сверткой функции
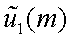 и
и
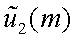 :
:
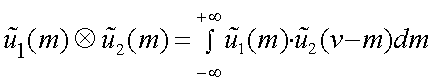 |
(4.28) |
Следовательно, имеем
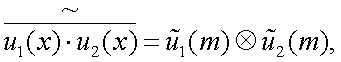
т.е. спектр произведения равен свертке спектров.
Е. Теорема о спектре свертки.
Рассмотрим свертку u(y) двух функций u1(x), u3(x):
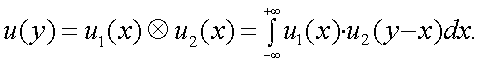
Спектр свертки u(y) равен
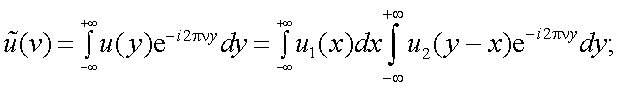
замена переменной: z = y - x
Тогда
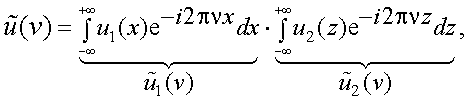
Откуда получаем
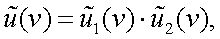 |
(4.29) |
т.е. спектр свертки двух функций равен произведению спектров этих функций.
Ж. Теорема о спектре производной сигнала.
Пусть спектр функции u(x) равен 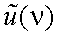 .
.
Найдем спектр 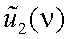 производной от заданной функции
производной от заданной функции 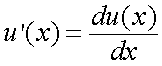 .
.
В соответствии с преобразованием Фурье имеем
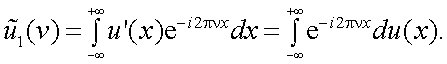 |
(4.30) |
Интегрируя (4.30) по частям, найдем:
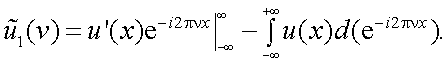
Так как функция u(x) → 0 при x → ± ∞, то
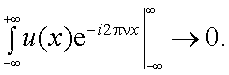
В то же время
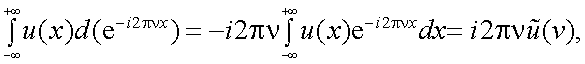
т.е. спектр производной равен спектру исходной функции, умноженному на i2πν.
З. Теорема о спектре интегрированного сигнала.
Пусть спектр функции u(x) равен 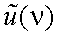 .
.
Найдем спектр 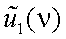 интеграла заданной функции в пределах от -∞ до +x, т.е.
интеграла заданной функции в пределах от -∞ до +x, т.е. 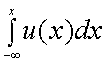 . Очевидно, что
. Очевидно, что
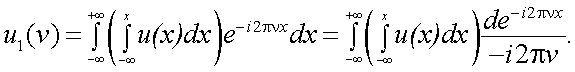 |
(4.31) |
Интегрируя (4.31) по частям, найдем:
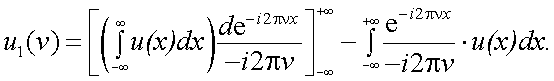
При условии, что 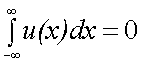 , найдем
, найдем
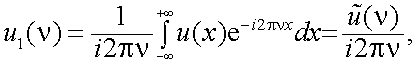
т.е. спектр интеграла заданной функции равен ее спектру, деленному на i2πν.
4.3. Случайные сигналы (спектры шумов) и способы их описания
Случайный сигнал (СС) может быть стационарным, когда его характеристики (математическое ожидание, дисперсия и др.) не зависят от аргумента спектральной функции. Основными характеристиками случайных функций являются: 1) плотность распределения вероятностей случайного процесса, 2) математическое ожидание, 3) дисперсия, 4) ковариационная и корреляционная функция, 5) энергетический спектр.
1. Плотность распределения вероятности случайного процесса. Если функция u(x) является случайной функцией аргумента x, то плотностью распределения непрерывной случайной величины u является функция
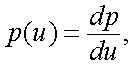 |
(4.32) |
так как dp = p(u)·du, т.е. вероятность dp попадания случайной величины u внутрь интервала du ~ величине интервала.
2. Математическое ожидание непрерывной случайной величины u равно:
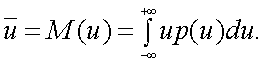 |
(4.33) |
3. Дисперсия случайной величины x
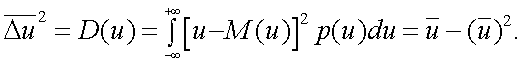 |
(4.34) |
4. Корреляционная функция случайного процесса u1(x), имеющего математическое ожидание M1(x) :
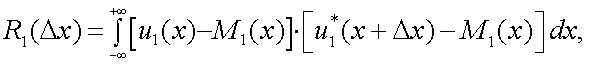 |
(4.35) |
где u1(x) – случайный процесс аргумента x.
Корреляционная функция обычно определяется, если u1(x) – центрированный случайный процесс. В других случаях пользуются понятием ковариационной функции K1(x):
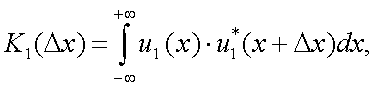 |
(4.36) |
которая, в нормированном виде, имеет вид:
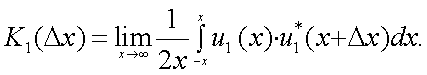
В тех случаях, когда анализируются два случайных процесса, имеет место понятие взаимно ковариационной функции процессов u1(x) и u2(x)
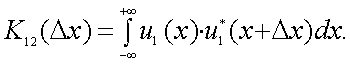 |
(4.37) |
5. В отличие от детерминированной функции (сигналов), преобразование Фурье к случайным функциям неприменимо, так как спектральная плотность самой спектральной функции – понятие бессмысленное. Можно ввести понятие о спектральной плотности дисперсии, так как последняя – неслучайная функция. Эта величина часто эквивалентна мощности, приходящейся на единицу частоты, поэтому ее называют энергетическим спектром случайной функции (статистическим спектром): 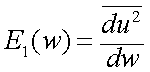 , откуда
, откуда 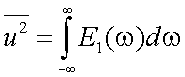 .
.
Н. Винер и А.Я. Хинчин показали для случайного стационарного процесса, что ковариационная функция K1(x) и энергетический спектр E1(ω) являются парой преобразований Фурье.
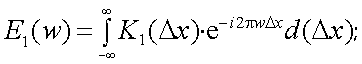 |
(4.38) |
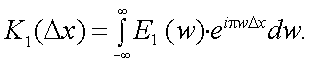 |
(4.39) |
Рассмотрим это подробнее.
Предположим, что задана функция u1(x), которая в интервале [-X, X] определяется:
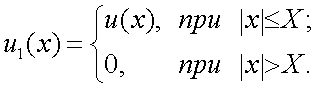
Найдем функцию автокорреляции рассматриваемой функции u1(x):
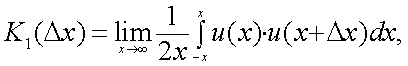 |
(4.40) |
где u(x) – центрированное значение функции u1(x).
Функции u(x) и u(x+Δx) можно представить в виде интегралов Фурье.
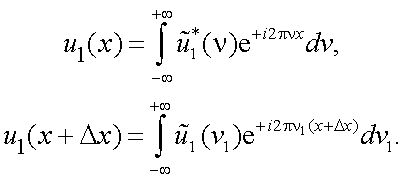 |
(4.41) |
Тогда
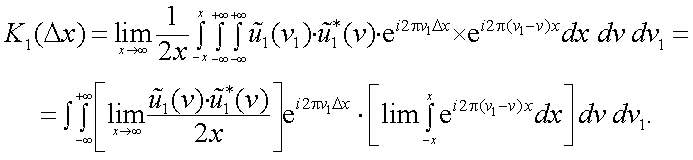 |
(4.42) |
Но внутренний интеграл в (4.42) представляет собой дельта-функцию:
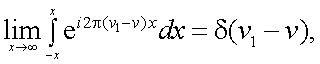
поэтому
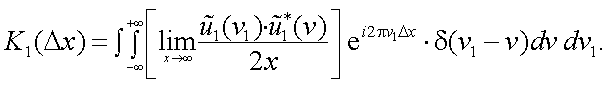
Так как δ(ν1-ν)≠0 при ν1=ν, то
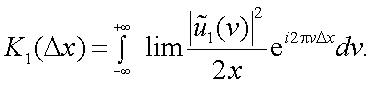
Обозначив
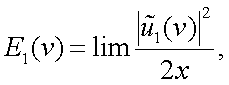
найдем
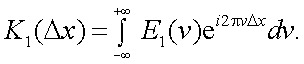
Поскольку K1(Δx) есть преобразование Фурье E1(ν), то справедливо и преобразование
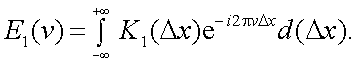 |
(4.43) |
Пользуясь зависимостью
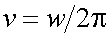 , получим
, получим
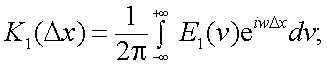 |
(4.44) |
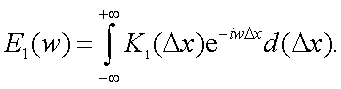 |
(4.45) |
Функцию E1(w) или (E1(ν)) называют энергетическим спектром, или спектром мощности случайного процесса u(x) . Это становится понятным из следующего:
при Δx = 0 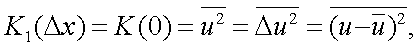 т.е. представляет собой дисперсию процесса.
т.е. представляет собой дисперсию процесса.
Поскольку 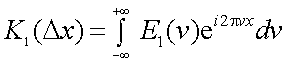 , то
, то 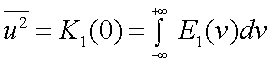 ; откуда имеем, что:
; откуда имеем, что:
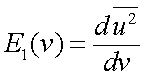 |
(4.46) |
представляет собой спектральную плотность дисперсии.
Двумерный спектр Хинчина – Винера для двумерного процесса имеет вид:
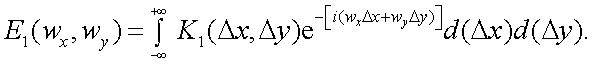 |
(4.47) |
Рассмотрим характерные случайные сигналы для ОЭП. Ими являются внутренние шумы приемников оптического излучения. Основные источники внешних случайных помех для ОЭП – излучение естественных фонов, на которых наблюдаются или исследуются объекты (излучение наземных ландшафтов, небесных тел, облаков и т.д.). В ряде случаев источником помех для ОЭП является искажающее влияние атмосферы на оптический сигнал, например, «мерцание» и «дрожание» изображения.
Иногда флуктуирующий излучающий фон представляют в виде случайной стационарной совокупности двумерных импульсов яркости, амплитуда которых подчиняется гауссовому (нормальному) закону распределения
[2]:
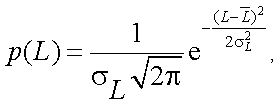 |
(4.48) |
а размеры участков фона – закону распределения Пуассона:
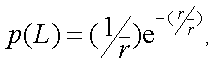 |
(4.49) |
где L – энергетическая яркость какой-либо точки фона;
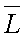 – средняя ее величина;
– средняя ее величина;
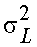 – дисперсия
L;
– дисперсия
L;
r – расстояние между отдельными точками фона;
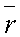 – средняя величина
r.
– средняя величина
r.
Если случайные величины L и r не зависят друг от друга, то двумерную автокорреляционную функцию можно записать в виде:
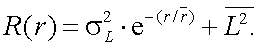 |
(4.50) |
Тогда, на основании преобразования Фурье, получим двумерный спектр мощности фона:
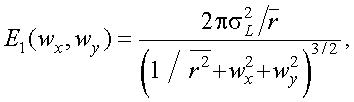 |
(4.51) |
где wx, wy – составляющие вектора пространственной частоты.
Одномерный спектр мощности определяется как
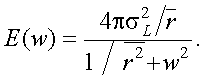 |
(4.52) |
Результаты современных статистических исследований фонов в области спектра Δλ = 2 – 3 мкм, где преобладает рассеянное солнечное излучение, показали, что распределение яркости городского ландшафта и неба подчиняются закону Пуассона. Во всех остальных случаях для фонов типа неба, лесного и городского ландшафтов это распределение подчиняется гауссовой статистике.
Для облачного изотропного фона в полярной системе координат спектр Хинчина – Винера иногда представляется в следующем виде [1]:
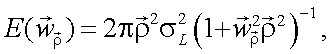 |
(4.53) |
где 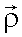 – радиус корреляции – параметр, аналогичный интервалу корреляции, на котором корреляционная функция составляет 0,37% от дисперсии яркости фона
– радиус корреляции – параметр, аналогичный интервалу корреляции, на котором корреляционная функция составляет 0,37% от дисперсии яркости фона 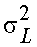 .
.
Для области высоких частот спектр Хинчина – Винера равен [1]:
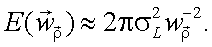 |
(4.54) |
Установлено, что случайная функция, описывающая фон неба, в общем случае нестационарна. Однако в пределах сравнительно небольших углов вдали от направлений на Солнце и на горизонт, фон облачного неба все же можно считать стационарным процессом. Радиус корреляции облачного неба обычно не превышает в угловой мере 1º ¸ 3º.

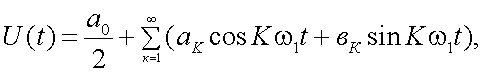
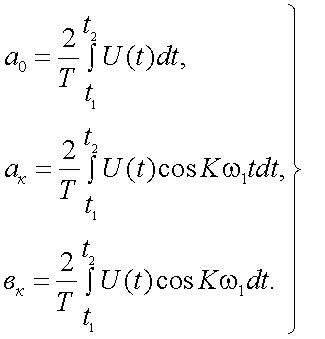
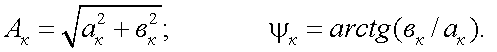
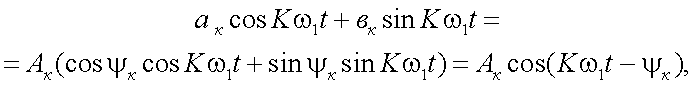
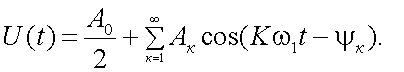
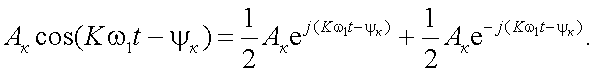
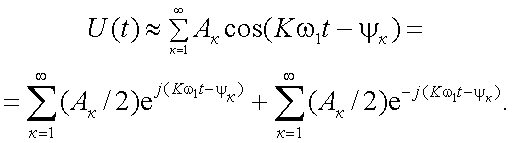
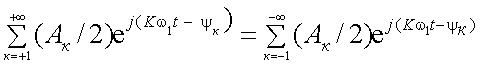
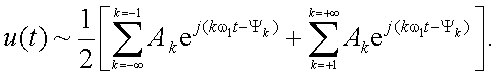
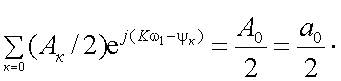
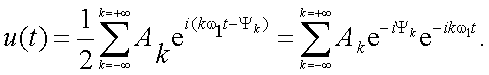
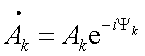 ,
,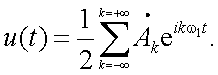
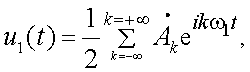
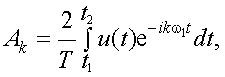
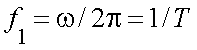 при T → ∞ стремится к 0, т. е. расстояние между спектральными линиями становится бесконечно малым, а спектр сплошным.
при T → ∞ стремится к 0, т. е. расстояние между спектральными линиями становится бесконечно малым, а спектр сплошным.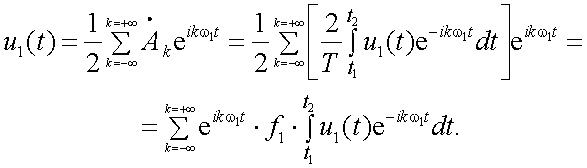
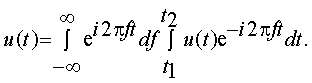
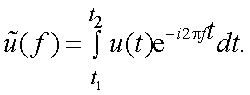
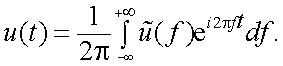
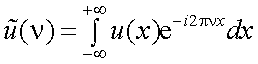
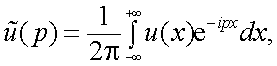
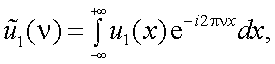
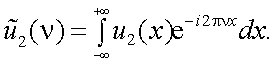
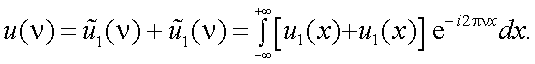
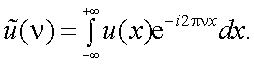
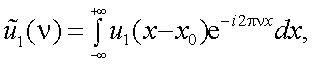
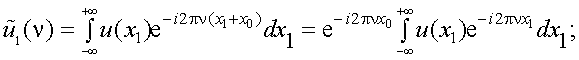
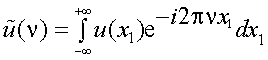
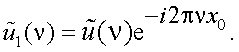
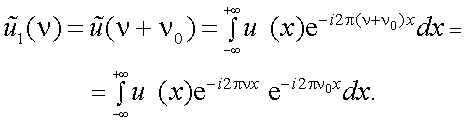
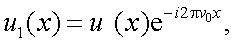 найдем
найдем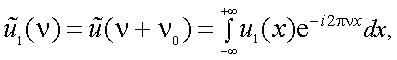
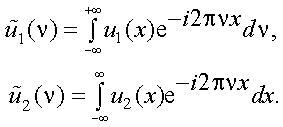
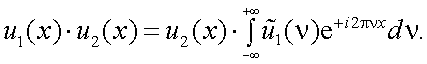
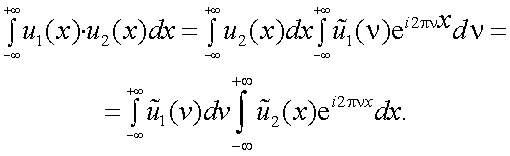
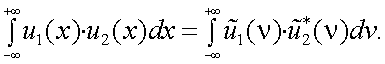
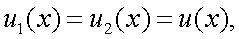 то
то 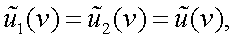 и
и 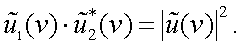
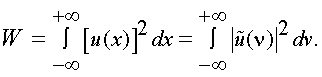
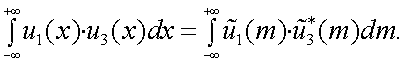
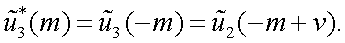
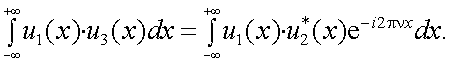
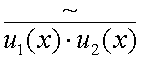 .
.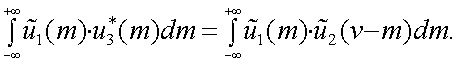
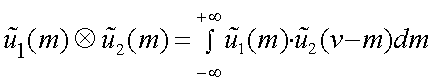
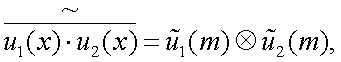
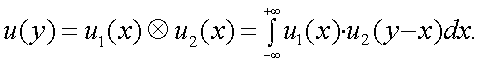
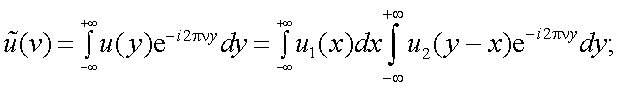
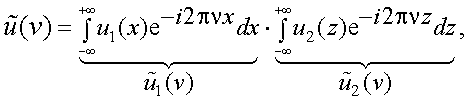
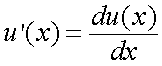 .
.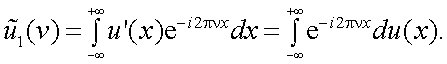
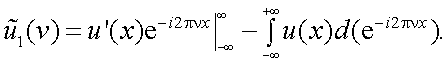
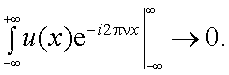
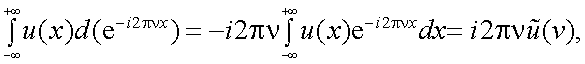
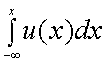 . Очевидно, что
. Очевидно, что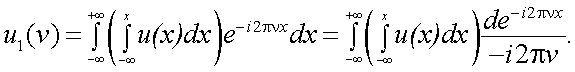
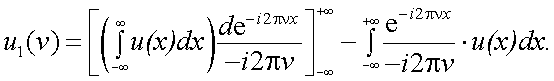
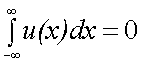 , найдем
, найдем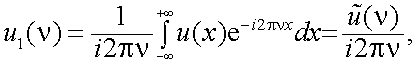
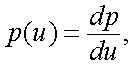
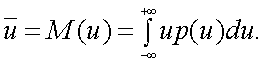
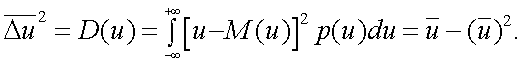
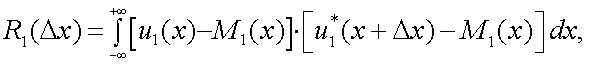
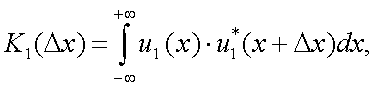
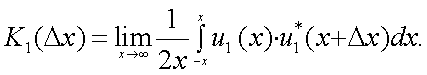
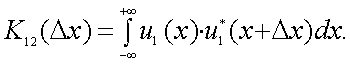
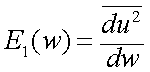 , откуда
, откуда 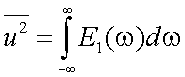 .
.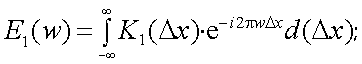
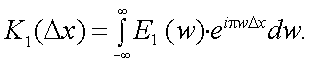
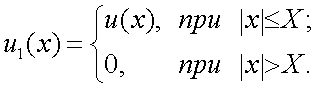
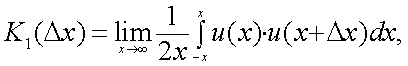
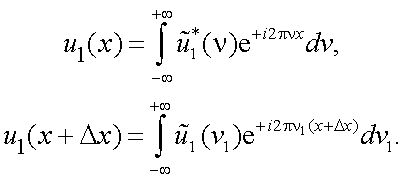
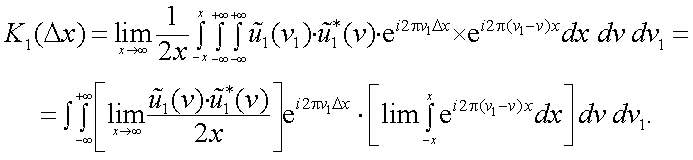
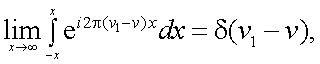
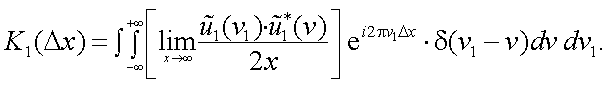
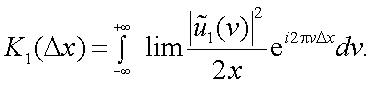
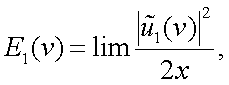
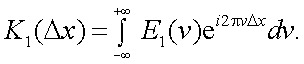
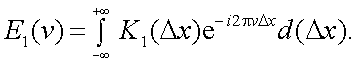
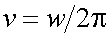 , получим
, получим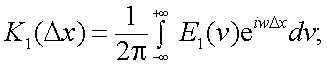
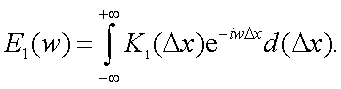
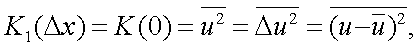 т.е. представляет собой дисперсию процесса.
т.е. представляет собой дисперсию процесса.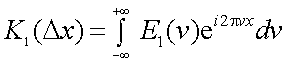 , то
, то 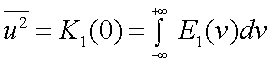 ; откуда имеем, что:
; откуда имеем, что: