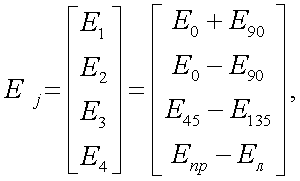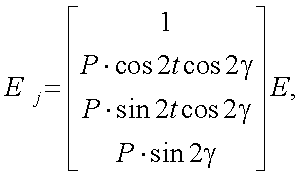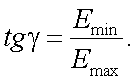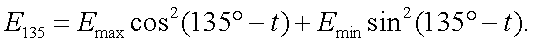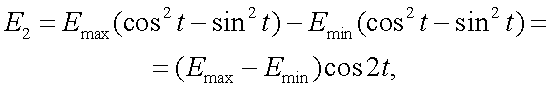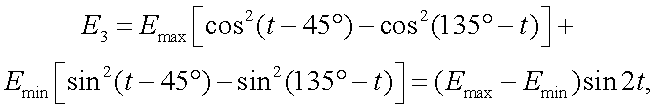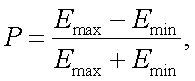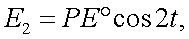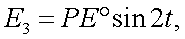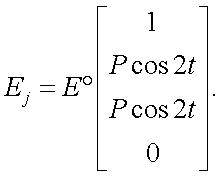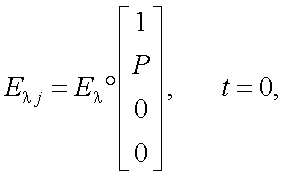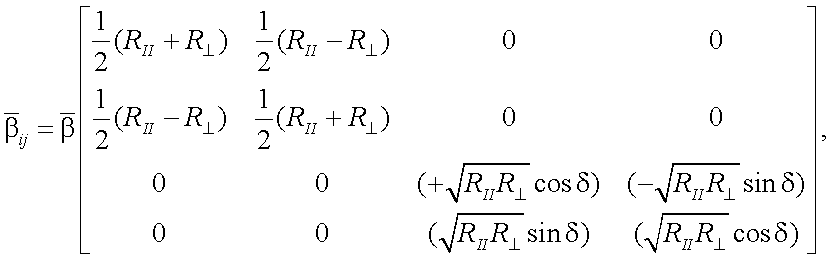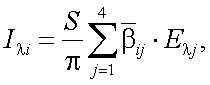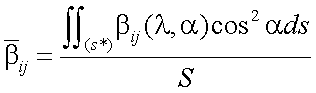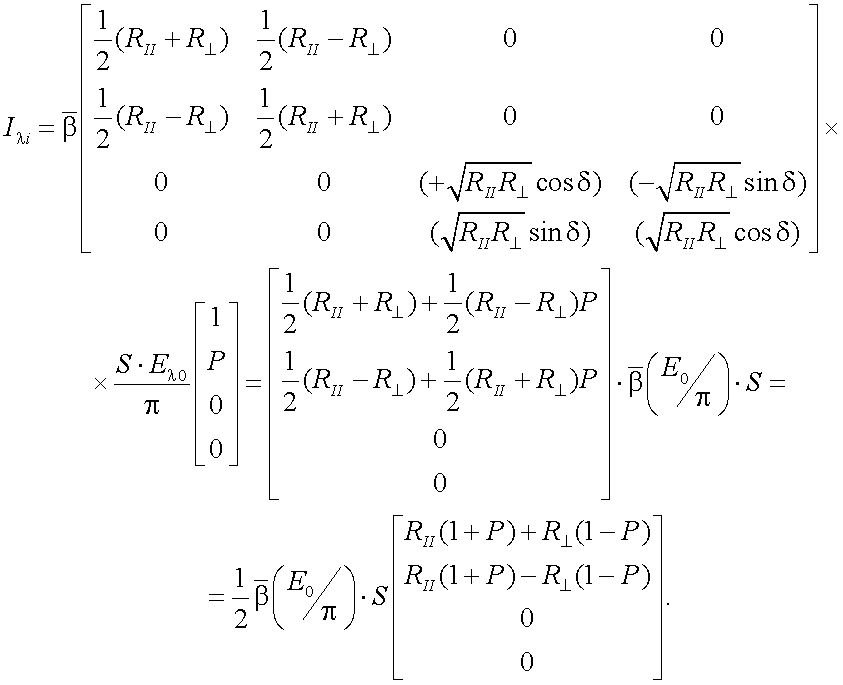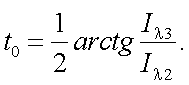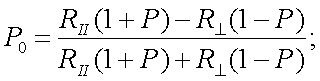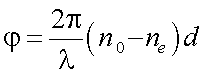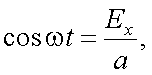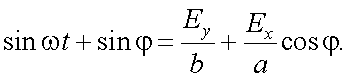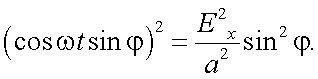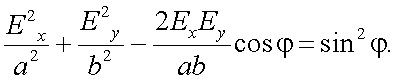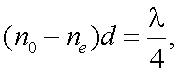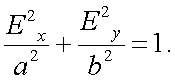Рассмотрим вектор-параметр Стокса оптического излучения [17]:
 |
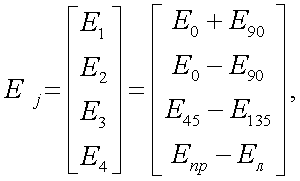(12.1) |
где Е0, Е45, Е90, Е135 – компоненты, поляризованные соответственно под углами 0, 45, 90 и 135° по отношению к плоскости референции;
Епр, Ел – право- и левоциркулярно поляризованные компоненты (рис. 12.1).
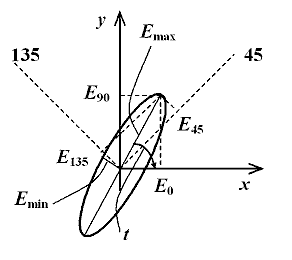
Рис. 12.1. Геометрия анализа поляризованного излучения
Для удобного вида в инженерной практике, при описании поляризованного излучения, его представляют в виде:
 |
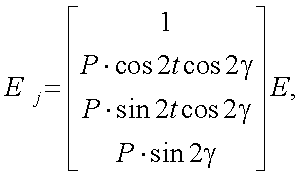(12.2) |
где P, t, γ – это степень, азимут и степень эллиптичности поляризации излучения.
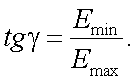
Согласно рис. 12.1 имеем:
 |
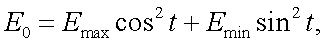
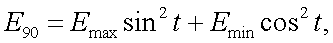(12.1,а) |
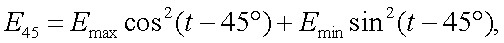
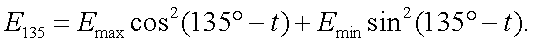
Так как для линейно поляризованного излучения, справедливо равенство:
 |
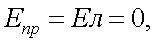(12.1,б) |
тогда, подставляя (а) и (б) в (12.1), имеем:
 |
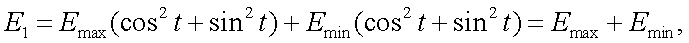
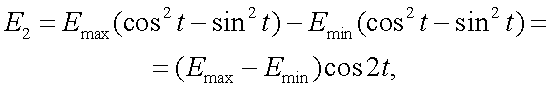
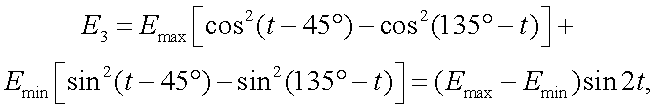(12.1,в) |
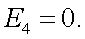
Воспользуемся теперь выражениями:
 |
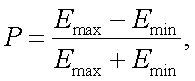(12.1,г) |
 |
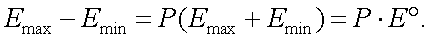(12.1,д) |
На основании формул (г) и (д), (в) принимает вид:
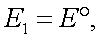
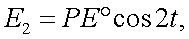
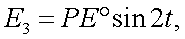
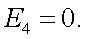
Вектор-параметр Стокса (12.1) можно записать в виде, идентичном (12.2):
 |
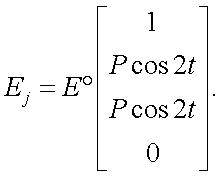(12.3) |
Для понимания сущности выражения (12.1) рассмотрим частный случай освещения объекта коллимированным пучком, вектор-параметр Стокса для освещенности которого в месте нахождения объекта имеет вид:
 |
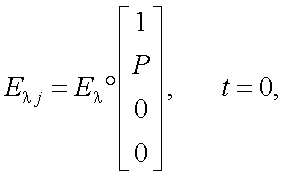(12.4) |
то есть объект освещается линейно поляризованным излучением с азимутом t = 0.
Допустим, что объект обладает матрицей отражения следующего вида:
 |
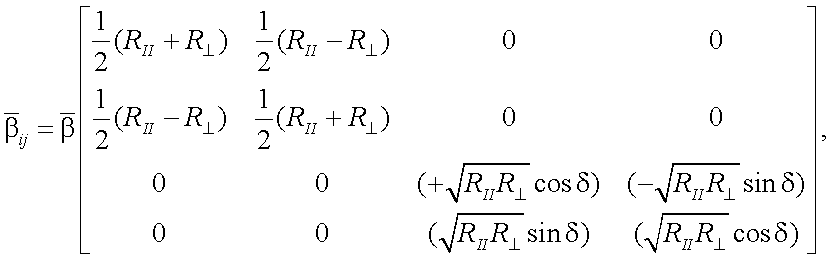(12.5) |
где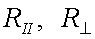 
– поляризационные компоненты френелевского коэффициента отражения, а разность фаз этих компонентов есть δ.
Выразим вектор-параметрическое представление в виде:
 |
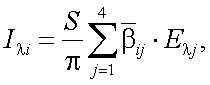(12.6) |
где
 |
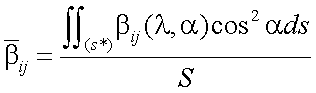(12.7) |
есть не что иное, как матрица отражения объекта [17].
Тогда, подставляя (12.4) и (12.5) в (12.6), компоненты вектор-параметра Стокса поляризованного отраженного излучения будут следующими:
 |
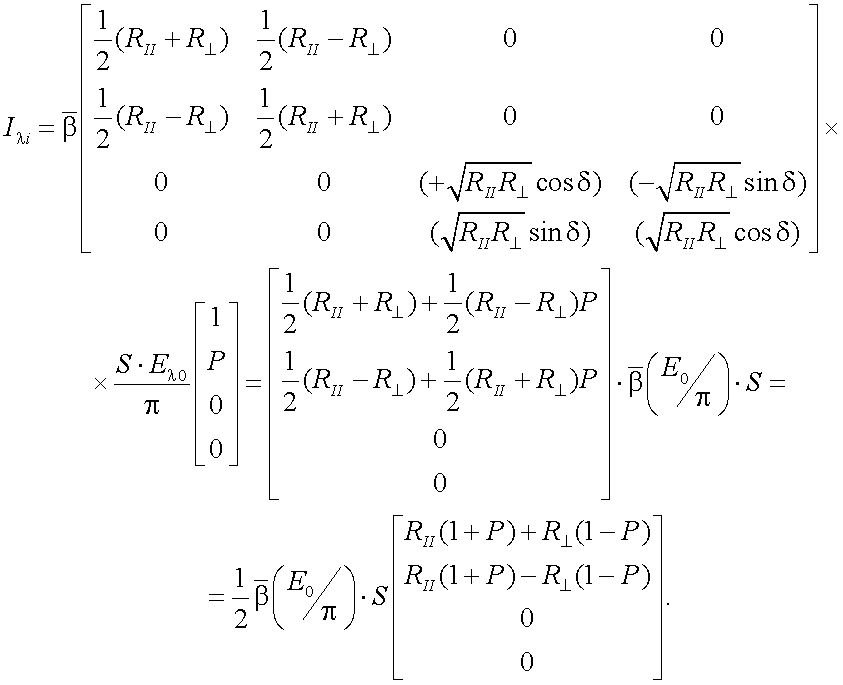(12.8) |
Выражение (12.8) позволяет определить степень и положение плоскости поляризации излучения объекта, если воспользоваться выражениями:
 |
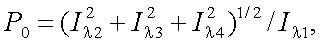(12.9) |
 |
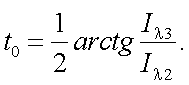(12.10) |
Тогда, подставив значения Iλ1, Iλ2, Iλ3, и Iλ4 в (14.9), а также Iλ2 и Iλ3 в (12.10), получим окончательное выражение для P0 и t0:
 |
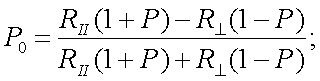(12.11) |
 |
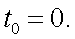(12.12) |
Таким образом, выражение (12.8) для отраженного излучения объектов при освещении их поляризованным излучением позволяет определить как общую энергию отраженного излучения, так и состояние поляризации, что подтверждают выражения (12.9) …(12.12).
Рассмотрим анализ эллиптически поляризованного света (рис. 12.2).
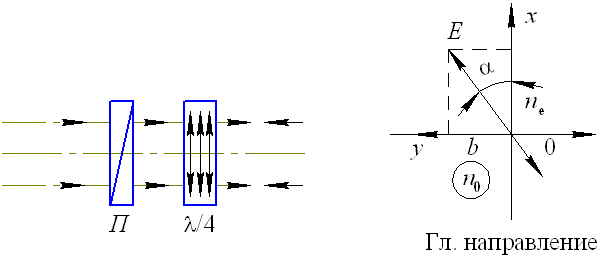
Рис. 12.2. К анализу эллиптически поляризованного света
Допустим, что на систему из пластинки λ/4 и линейного поляризатора П падает эллиптически поляризованный свет.
Тогда имеем:
 |
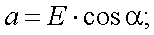(12.13) |
 |
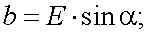
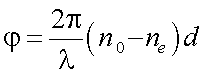(12.14) |
– разность фаз между обыкновенной и необыкновенной волнами в поляризационном кристалле.
Значит:
 |
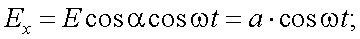(12.15) |
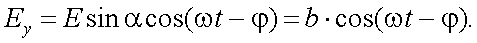
Чтобы получить траекторию результирующего колебания, исключим время t:
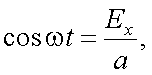
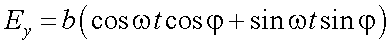
или
 |
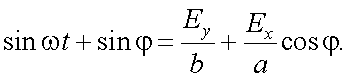(12.16) |
Возводим (12.16) в квадрат и суммируем его с выражением:
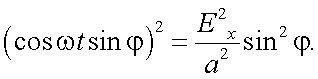
Тогда получим:
 |
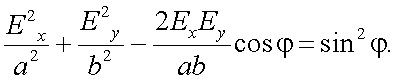(12.17) |
Анализируя (12.17), можно отметить, что форма и ориентация эллипса зависит от углов α и φ.
Рассмотрим действие пластинки λ/4.
Оптическая разность хода в этом случае равна:
 |
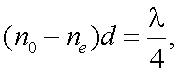(12.18) |
тогда
 |
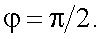(12.19) |
Подставив (12.19) в (12.17), получим:
 |
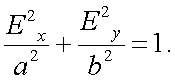(12.20) |
Эллипс ориентирован вдоль осей OX и OY.
Если α = 45°, то a = b и получаем:
 |
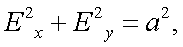(12.21) |
т. е. имеем свет циркулярный.
Если φ = π/2 , то Ex опережает Ey по фазе на π/2.
Если φ = -π/2 , то Ex тстает от Ey на π/2по фазе.
В соответствии с этим, результирующий вектор вращается против часовой стрелки (влево) или по часовой стрелки (вправо). Поэтому и принято различать левую и правую эллиптическую и циркулярную поляризацию.
