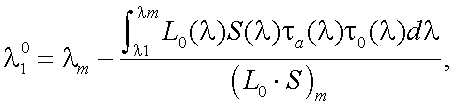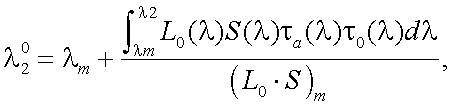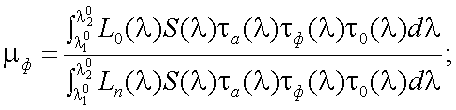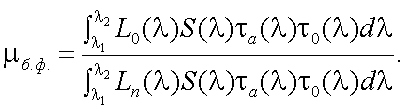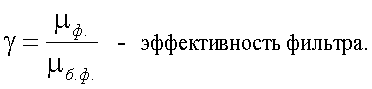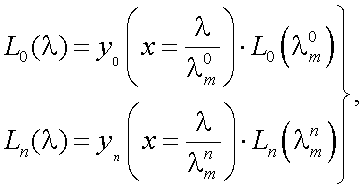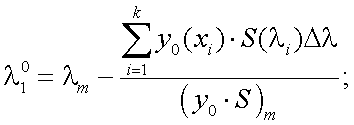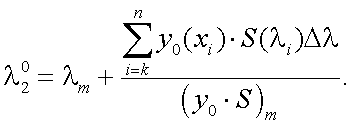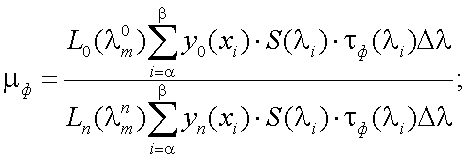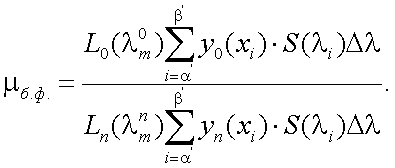11.1. Эффективная спектральная ширина полосы пропускания фильтра
Принцип спектральной фильтрации чаще всего состоит в выборе такого рабочего участка λ1…λ2 оптического спектра, для которого на выходе приемника излучения ОЭП отношение сигнала от наблюдаемого объекта к сигналу от помех является наибольшим. Оптимальная спектральная фильтрация возможна только при одновременном учете спектральных характеристик объектов, фонов и приемников излучения, а также оптических сред, расположенных между объектом и ОЭП. Приведенные выше положения общей теории оптимальной фильтрации полностью приемлемы к этому случаю.
Рассмотрим спектральную фильтрацию оптического излучения объекта, имеющего спектральную плотность энергетической яркости (СПЭЯ) L0(λ). При этом известны спектральные характеристики помехи, приемника оптического излучения, оптических элементов ОЭП и среды распространения излучения (рис. 11.1):
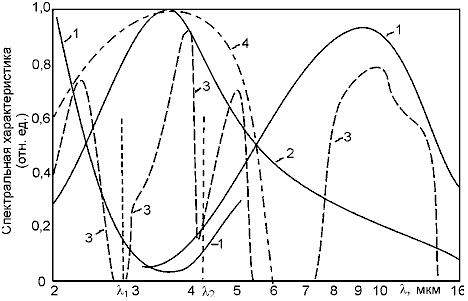
Рис. 11.1. К объяснению спектральной фильтрации:
1 – спектральная плотность энергетической яркости излучения помехи (Lп(λ));
2 – спектральная плотность энергетической яркости излучения объекта (L0(λ));
3 – спектральный коэффициент пропускания слоя атмосферы (τа(λ));
4 – спектральная чувствительность приемника излучения (S(λ))
Согласно данным работы [1], расчет качества спектральной фильтрации можно осуществить с помощью понятия эффективной спектральной ширины полосы пропускания фильтра:
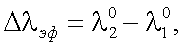
где
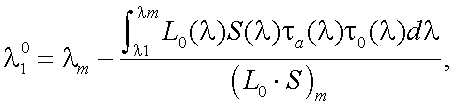 |
(11.1) |
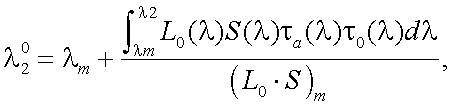 |
(11.2) |
λ1, λ2 – границы чувствительности приемника.
Для определения эффективности спектрального фильтра находим отношение «сигнал/помеха» с использованием фильтра (μф) и без него (μб.ф):
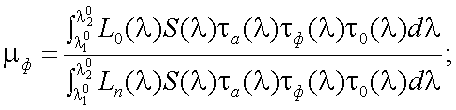 |
(11.3) |
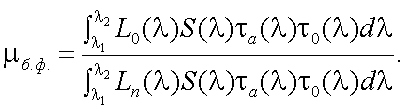 |
(11.4) |
Тогда
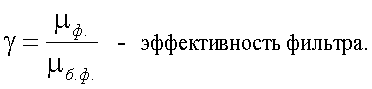 |
(11.5) |
Если γ > 1 , то спектральный фильтр эффективен.
Рассмотрим частный случай, когда объект и фон излучают с температурой Т0 ~ Тп.
Допустим, что τa(λ) = τ0(λ) = 1.
Так как
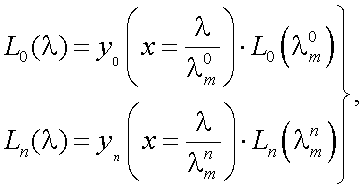 |
(11.6) |
тогда, выражение (11.1) и (11.2), если интеграл заменить суммой, примет вид:
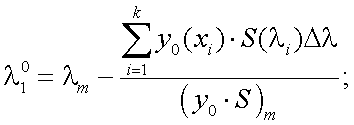 |
(11.7) |
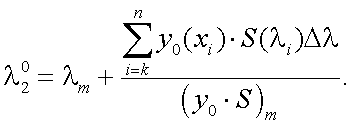 |
(11.8) |
Индекс i принимает значения 1, k, n, что соответствует длинам волн λ1, λm и λ2, где λ1 и λ2 – левая и правая границы чувствительности приемника излучения, а λm соответствует максимальному значению выходного сигнала приемника.
Применительно для формулы (11.3) и (11.4) имеем:
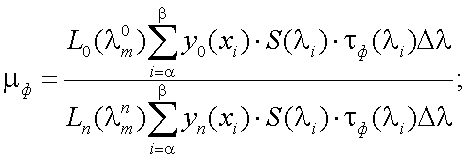 |
(11.9) |
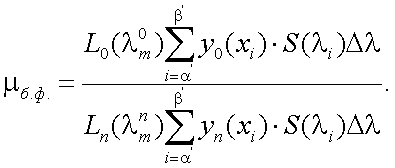 |
(11.10) |
Аналогично, что при значениях индекса i = α, β, α' и β' длины волн соответствуют следующим значениям:
λ01 и λ02 – левая и правая границы спектрального фильтра;
λ1 и λ2 – левая и правая границы чувствительности приемника излучения.