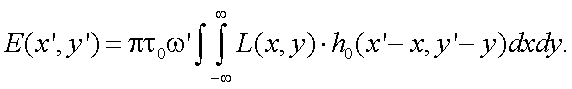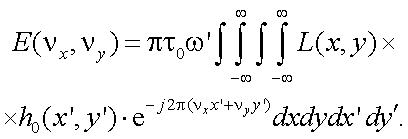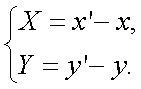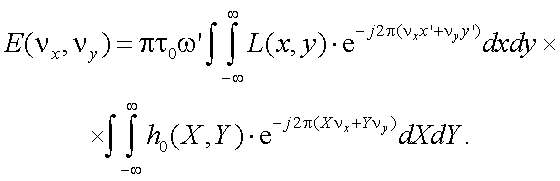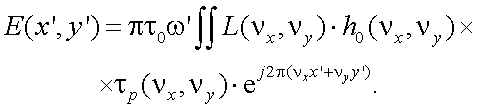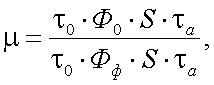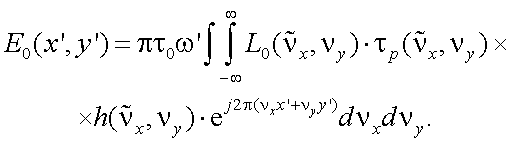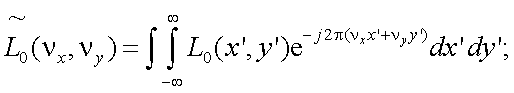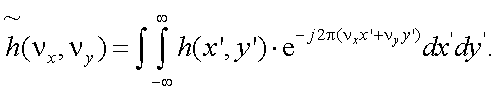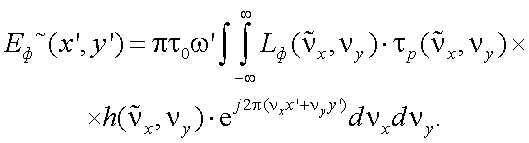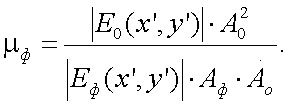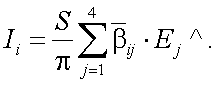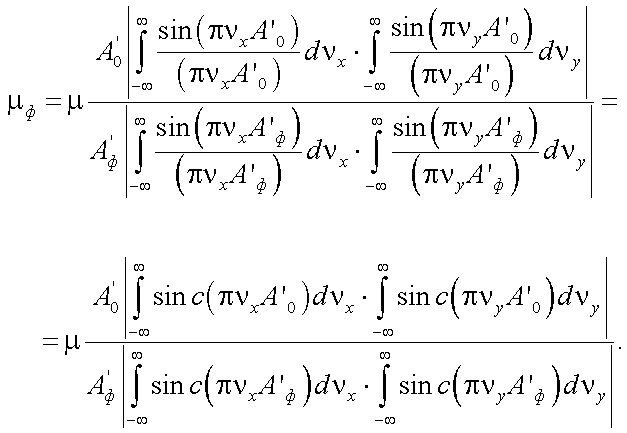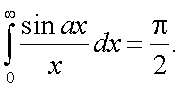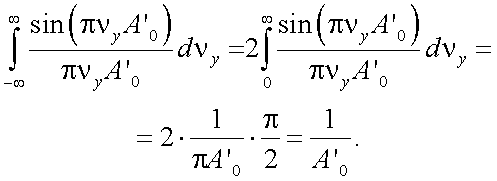10.1. Классификация оптических фильтраций
Носителями информации в оптико-электронных приборах служит оптическое излучение, идущее от исследуемого объекта. Основными параметрами этого полезного оптического излучения являются длина волны, поляризационные характеристики, интенсивность (амплитуда) и их пространственное распределение, которое характеризует форму и размеры исследуемого объекта. Каждый из перечисленных параметров может нести полезную информацию об исследуемом объекте.
Аналогичными параметрами можно характеризовать и излучение от других предметов, на фоне которых производится наблюдение исследуемого объекта. Излучение от этих предметов создает помеху, искажающую полезную информацию об исследуемом объекте.
При проектировании оптико-электронных систем (ОЭC) проводится предварительное изучение параметров излучений исследуемого объекта и фона, а также выбор в качестве основного параметра сигнала такого параметра излучения, который в большей степени характеризует исследуемый объект и в меньшей степени – вредный фон. Использование фильтров позволяет выделить сигнал из смеси «сигнал-помеха», поступающей на вход оптико-электронной системы, и, тем самым, улучшить ее информационно-измерительные характеристики.
По виду основного информационного параметра оптического сигнала фильтрации подразделяют на спектральную, поляризационную и пространственную [1 – 4].
Спектральная фильтрация заключается в использовании спектральных фильтров, пропускающих на фотоприемник оптическое излучение в заданном интервале длин волн.
Пространственная фильтрация характеризуется использованием в качестве информационного параметра пространственного распределения интенсивности излучения, которое выделяется из смеси «сигнал-помеха» с помощью пространственно-частотных фильтров, выполненных в виде щелей, масок, растров, фурье-голограмм. Пространственная фильтрация широко используется в задачах поиска, обнаружения, распределения и контроля объектов заданной формы.
Поляризационная фильтрация заключается в применении фильтров, пропускающих на фотоприемник излучение определенной поляризации для объектов и не пропускающих поляризованное излучение помех.
10.2. Пространственная фильтрация в ОЭП и С
Рассмотрим пространственную фильтрацию излучения объекта и фонов в ОЭП и С (рис. 10.1).
Рис. 10.1. К теории изображений в оптических системах с использованием свертки
На основании рис. 10.1 освещенность в окрестности площадки dS' равна:
 |
(10.1) |
Суммарная освещенность, формируемая за счет излучения всей поверхности объекта, равна:
 |
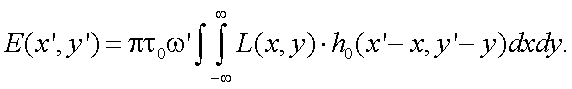(10.2) |
Пространственно-частотный спектр изображения объекта имеет вид:
 |
(10.3) |
Подставив в (10.3) соотношение (10.2), получаем:
 |
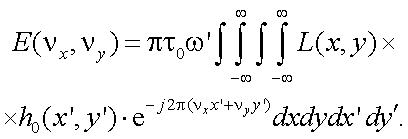(10.4) |
Введем замену переменных:
 |
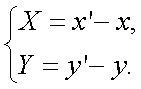(10.5) |
Тогда, с учетом (10.5), (10.4) принимает вид:
 |
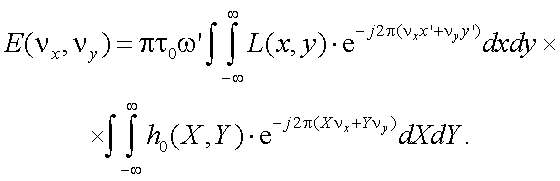(10.6) |
В итоге получаем:
 |
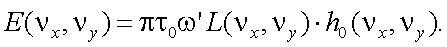(10.7) |
Если в плоскости изображения поместим растр, то спектр принимает вид:
 |
(10.8) |
 |
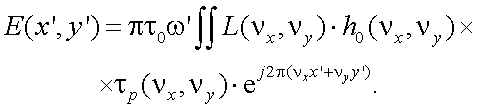(10.9) |
Здесь E(νx, νy) и Ep(νx, νy) – пространственно-частотные спектры изображения объекта в плоскости изображения и после растра с передаточной функцией τ0(νx, νy); Ep(x', y') – освещенность в изображении объекта после пространственной фильтрации растром.
10.3. Теория пространственно-частотной фильтрации. Отношение «сигнал/помеха» в ОЭП и С с пространственно-частотными фильтрами
Допустим, что ОЭП обнаружения с квадратным полем зрения имеет фокусное расстояние f′ и апертурный угол ω. На расстояние l поле зрения ОЭП охватывает участок фона с разрешением Аф × Аф. В поле зрения находится еще излучающий объект (цель) с размерами А0 × A0. В фокальной плоскости объектива ОЭП располагается растр в виде щелевой диафрагмы, ширина A'0 которой равна размеру изображения объекта. После растра располагается приемник излучения, размер чувствительной площадки которого равен А′ф × А′ф. Чувствительная площадка сопряжена с участком фона Аф × Аф. В случае работы ОЭП обнаружения без анализатора изображений (растра), отношение «сигнал/помеха» можно рассчитать по формуле:
 |
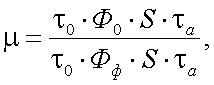(10.10) |
где Ф0, Фф – интегральный поток излучения объекта и фона.
С учетом яркости объекта и фона выражение (10.10) принимает следующий вид:
 |
(10.11) |
где L0, Lф – интегральная яркость излучения объекта и фона;
T0, Tф – температура объекта и фона;
S – интегральная чувствительность приемника излучения;
τ0 – интегральный коэффициент пропускания оптических элементов;
τа – интегральный коэффициент пропускания слоя атмосферы между объектом и прибором.
При введении анализатора изображений (растра) в качестве пространственно-частотного фильтра, если размеры объекта и фона различны, то отношение «сигнал/помеха» можно существенно увеличить. Этот эффект рассмотрим на основе следующих рассуждений.
Согласно дифракционной теории формирования изображений с учетом пространственно-частотных спектров (ПЧС) объекта и фона, а также пространственно-частотной передаточной функции (ПЧПФ) растра и оптической передаточной функции оптической системы, освещенность в изображении объекта и фона после растра можно представить в виде [1]:
 |
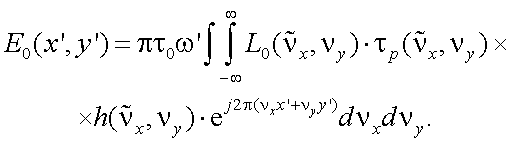(10.12) |
 |
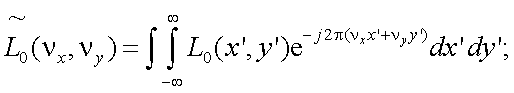(10.13) |
 |
(10.14) |
 |
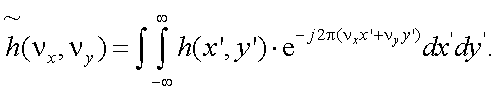(10.15) |
Здесь ω′ – задний апертурный угол оптической системы ОЭП;
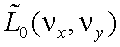– ПЧС объекта в пространстве изображений;
– ПЧПФ растра;
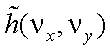– оптическая передаточная функция (ОПФ) оптической системы;
– функция рассеяния оптической системы;
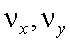– пространственные частоты в пространстве изображений.
Выражение (10.12) показывает следующее.
1. Оптическая система осуществляет двумерное обратное преобразование Фурье произведения спектра яркости излучения объекта и ПЧС оптической системы растра.
2. Освещенность изображения объекта после растра есть не что иное, как двумерное обратное преобразование Фурье произведения ПЧС объекта, ОПФ оптической системы и ПЧПФ растра.
3. ПЧС освещенности изображения есть произведение ПЧС яркости объекта, ОПФ оптической системы и ПЧПФ растра:
 |
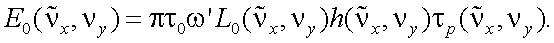(10.16) |
Аналогично для фона можно записать:
 |
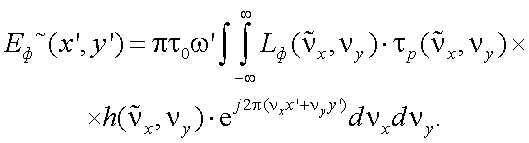(10.17) |
Согласно работе [2], качество фильтрации оценивается отношением «сигнал/помеха» с пространственным фильтром (растром) по формуле:
 |
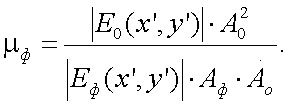(10.18) |
В случае безаберрационных оптических систем, когда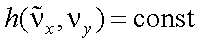 
, и с учетом выражений (10.12) и (10.17), формула (10.18) может быть записана в виде:
 |
(10.19) |
Применив к числителю и знаменателю в (10.19) неравенство Буняковского – Шварца [12], последнее запишем в виде:
 |
(10.20) |
Рассмотрим случай, когда объект и фон являются тепловыми излучателями. Тогда:
 |
(10.21) |
 |
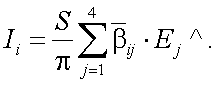(10.22) |
Здесь T0, Tф – температура объекта и фона соответственно.
Тогда отношение «сигнал/помеха», когда растр является щелевой диафрагмой с размерами A'0 · A'ф, будет следующим (так как (A'0/A'ф)2 = (A0/Aф)2):
 |
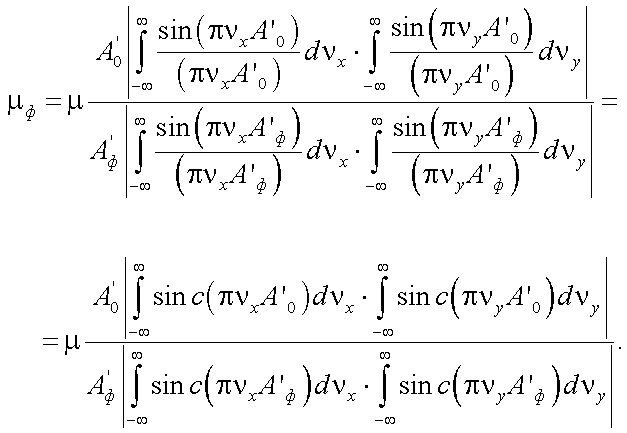(10.23) |
При расчете следует принять во внимание следующее. Из справочника [29] имеем:
 |
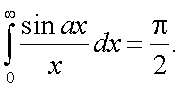(10.24) |
Тогда:
 |
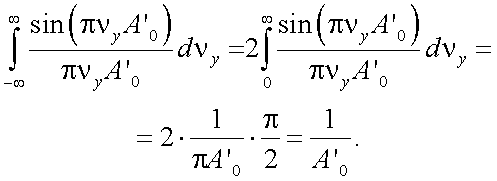(10.25) |
