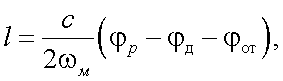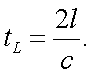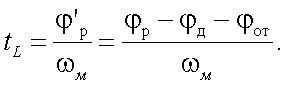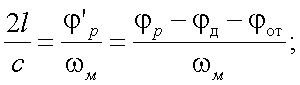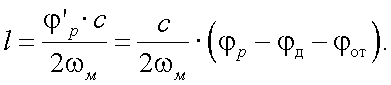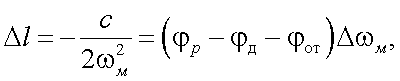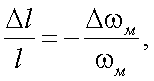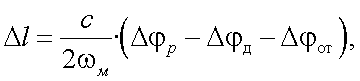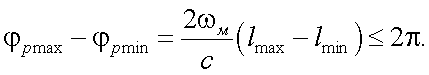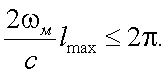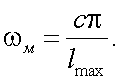Принцип действия фазового оптического дальномера, упрощенная схема которого приведена на рис. 26.1, сводится к следующему. Излучение ОКГ модулируется генератором масштабной частоты, причем напряжение на модуляторе и, следовательно, выходное излучение промодулированного в соответствии с законом, определится по формуле:
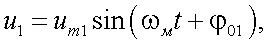 |
(26.1) |
где ωм – масштабная частота;
φ01 – начальная фаза.
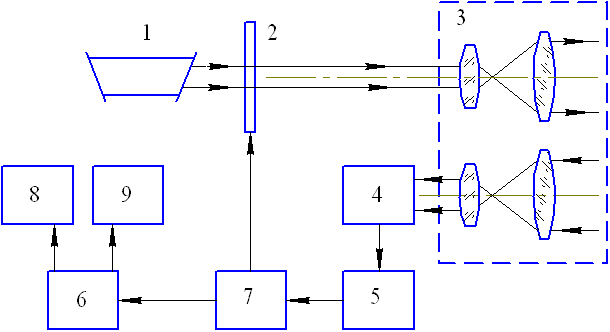
Рис. 26.1. Блок-схема оптико-электронного локатора с ОКГ, работающего на фазовом методе:
1 – ОКГ; 2 – модулятор; 3 – приемно-передающие оптическая система локатора; 4 – ФЭУ; 5 – усилитель; 6 – фазометр; 7 – генератор модулятора; 8 – индикатор дальности; 9 – индикатор скорости
Отразившись от цели, излучение попадает на приемно-передающее устройство оптического дальномера, которое преобразует его в электрический сигнал:
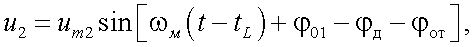 |
(26.2) |
где φот – угол сдвига фазы масштабного колебания, возникающий при отражении от объекта сложной формы;
φд – запаздывание фазы масштабного колебания в цепях оптического дальномера.
Напряжения u1 и u2 поступают на вход фазометра, который в соответствии с разностью фаз выдаст сигнал, пропорциональный дальности l:
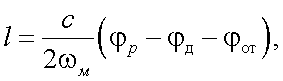 |
(26.3) |
где
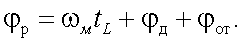 |
(A) |
Вывод: согласно (26.1) и (26.2) разность фаз сигналов u1 и u2 соответствует выражению (А).
С одной стороны, справедливо равенство:
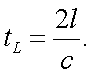 |
(Б) |
С другой стороны, согласно (А), имеем:
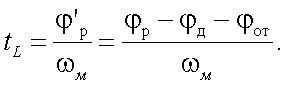 |
(В) |
Тогда, приравнивая (Б) и (В), получаем:
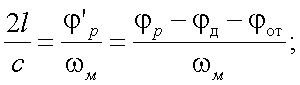 |
(Г) |
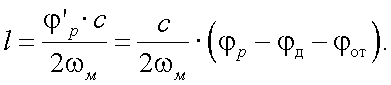 |
(26.3') |
Точность работы дальномера определяется:
1) точностью масштабной частоты:
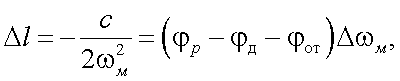 |
(26.4) |
где ωм – ошибка масштабной частоты.
Тогда, на основании (26.4) и (26.3), имеем:
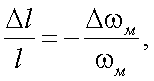 |
(26.5) |
то есть относительная дальномерная ошибка равна относительной ошибке масштабной частоты;
2) точностью измерения разности фаз.
Можно записать, что
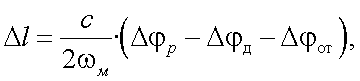 |
(26.6) |
где Δφp – ошибка в измерении разности фаз;
Δφд – ошибка запаздывания фазы в цепях дальномера;
Δφот – ошибка сдвига фазы при отражении.
Составляющая Δφp определяется техническими параметрами фазометра. Составляющая Δφд зависит от стабильности фазовой характеристики дальномера, составляющая Δφот – от того, на сколько точно учтены отражательные свойства цели. При измерении расстояния до подвижной цели вносится еще одна ошибка, источником которой является частота Доплера. Исследования показывают, что вторая и третья составляющие в выражении (26.6) являются величинами второго порядка малости по сравнению с первой, поэтому в расчетах ими можно пренебречь. Из анализируемого выражения можно сделать еще один вывод о том, что дальномерная ошибка уменьшается с ростом масштабной частоты. Можно отметить, что переход к более коротким длинам волн дает выигрыш в повышении точности измерений. Но это имеет и свою отрицательную сторону. Дело в том, что однозначность при измерении разности фаз возможна только в пределах угла 2π, в противном случае возникает многозначность отсчета дальности. Для того, чтобы избежать многозначности отсчета, необходимо выполнить условие:
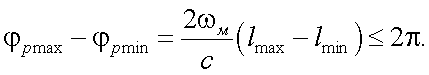 |
(26.7) |
При Lmin это условие принимает вид:
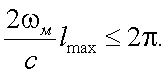 |
(26.8) |
Это выражение дает возможность определить максимальное значение масштабной частоты:
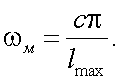 |
(26.9) |
Таким образом, для повышения точности измерений необходимо увеличить масштабную частоту, а для выполнения условия однозначности измерений ее необходимо уменьшить. Выход из этого положения обычно таков: использую две, а иногда и три масштабные частоты. Первая служит для грубого определения дальности, вторая – для более точного, а третья для еще более точного измерения дальности.