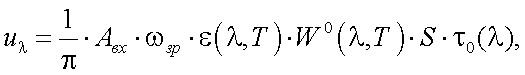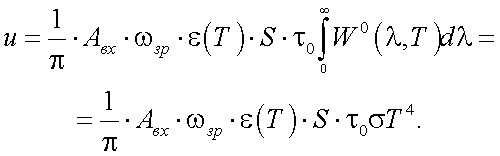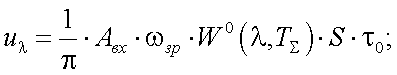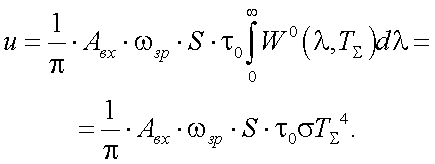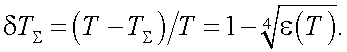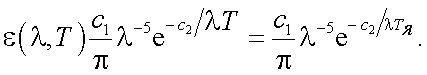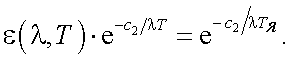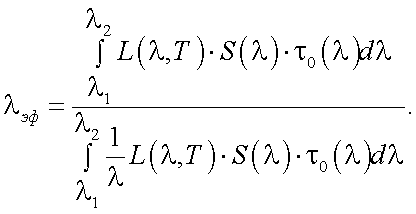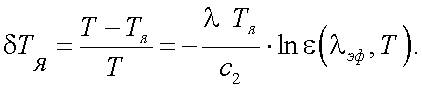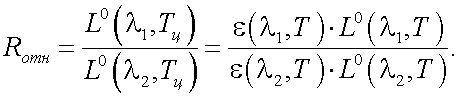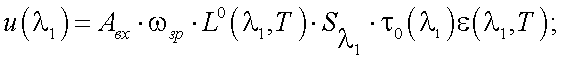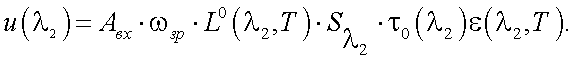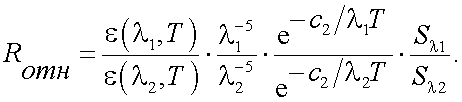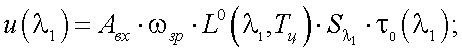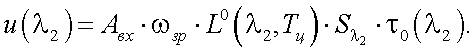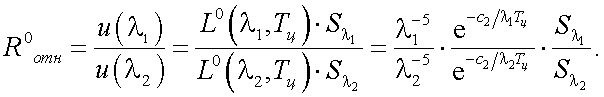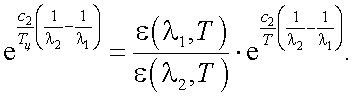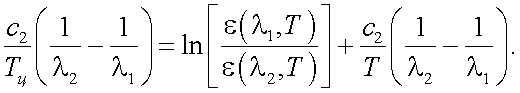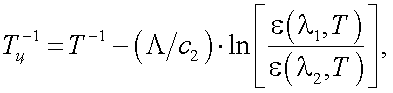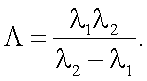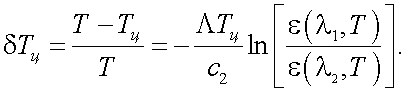Из закона Планка следует, что температура тела T влияет на плотность излучения суммарного потока, его спектральные составляющие и на спектральное распределение. В связи с этим можно выделить три метода радиационной пирометрии, основанных на измерении суммарного излучения, его плотности в некотором спектральном интервале, а также отношение плотностей излучения в различных участках спектра [40].
1. Первый метод – метод энергетической температуры или полной радиации.
Для реального тела спектральная светимость равна:
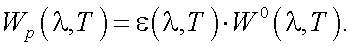 |
(39.1) |
Если абсолютная спектральная чувствительность S приемника не зависит от λ, то сигнал на выходе приемника излучения пирометра равен:
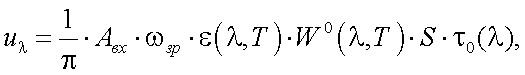 |
(39.2) |
где Aвх – площадь входного зрачка пирометра;
ωзр – телесный угол поля зрения пирометра;
τ0(λ) – спектральный коэффициент пропускания оптической системы пирометра;
ε(λ, T) – коэффициент излучения материала тела.
Суммарный сигнал приемника излучения при ε(λ, T) = ε(T) равен:
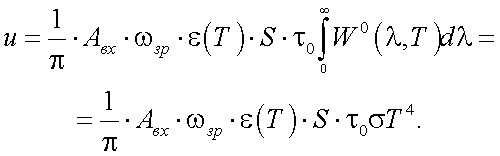 |
(39.3) |
Для АЧТ с температурой TΣ имеем:
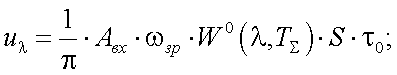 |
(39.4) |
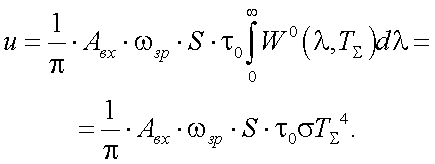 |
(39.5) |
Приравняв (39.3) и (39.5), получим:
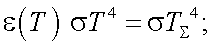 |
(39.6) |
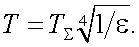 |
(39.7) |
Отклонение истинной температуры Т от радиационной TΣ равно:
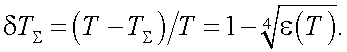
2. Второй метод – метод частичной радиации (метод яркостной температуры).
Для реального тела с температурой Т спектральная яркость объекта равна:
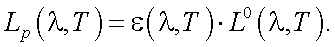 |
(39.8) |
Тогда выходной сигнал с приемника излучения яркостного пирометра равен:
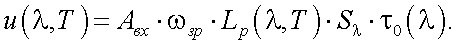 |
(39.9) |
Для АЧТ с яркостной температурой Тя и спектральной яркостью L0(λ, Tя) сигнал на выходе приемника излучения равен:
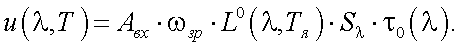 |
(39.10) |
Приравняв (39.9) и (39.10), имеем:
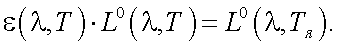 |
(39.11) |
В приближении Вина для спектральной яркости АЧТ соотношение (39.11) имеет вид:
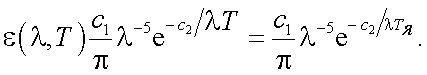 |
(39.12) |
После упрощений (39.12) приобретает вид:
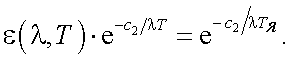 |
(39.13) |
Прологарифмировав (39.13), имеем:
 |
(39.14) |
Решая уравнение (39.14) относительно Тя, получаем:
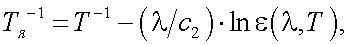 |
(39.15) |
где Тя – яркостная температура.
Так как пирометр работает в достаточно широком спектральном интервале ∆λ, то формулы (39.8) … (39.15) справедливы на, так называемой, эффективной длине волны λэф:
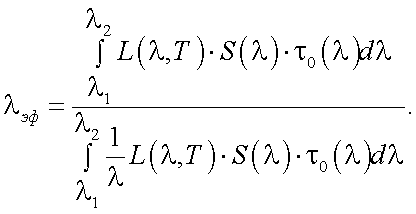 |
(39.16) |
Методическая погрешность метода равна:
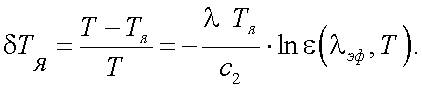 |
(39.17) |
3. Третий метод – метод цветовой температуры (или спектрального отношения).
Введем величину:
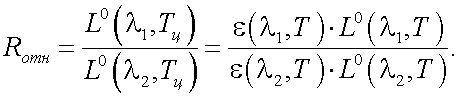 |
(39.18) |
Это критерий определения цветовой температуры.
При наблюдении пирометром объекта, выражения для сигналов на выходе приемника излучения при нахождении соответственно первого и второго спектрального фильтров в поле зрения прибора, равны:
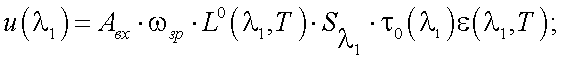 |
(39.19) |
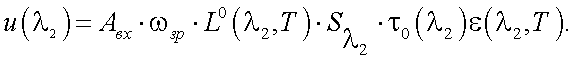 |
(39.20) |
Если τ0(λ1) = τ0(λ2), то в приближении Вина имеем:
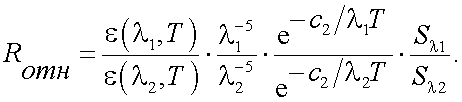 |
(39.21) |
Для АЧТ соответствующее значение сигналов u(λ1) и u(λ2) равны:
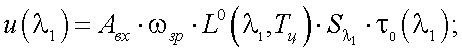 |
(39.22) |
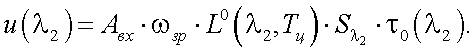 |
(39.23) |
Параметр R0отн для АЧТ равняется:
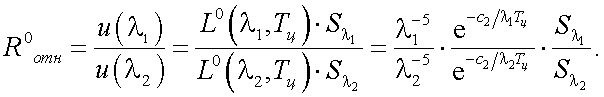 |
(39.24) |
Приравняв (39.21) и (39.24), получим:
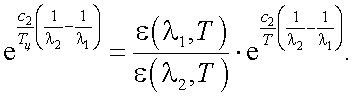 |
(39.25) |
Прологарифмировав выражение (39.25), получим следующее уравнение:
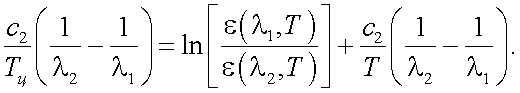
Решение уравнения (39.25) дает следующее выражение для температуры Тц:
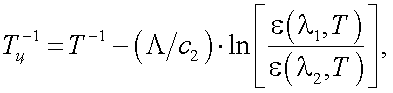 |
(39.26) |
где
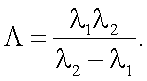
Методическая ошибка метода равна:
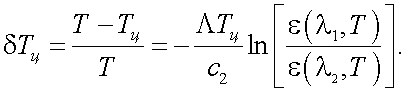 |
(39.27) |