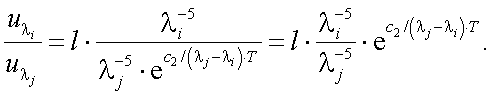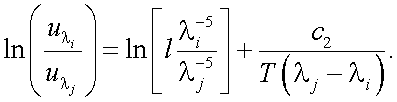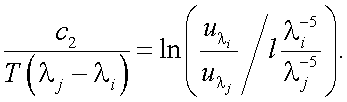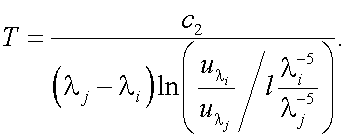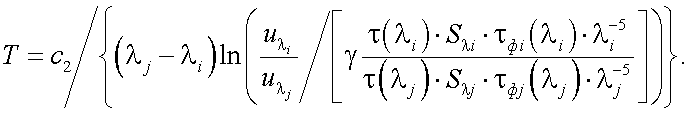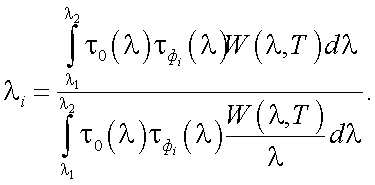Метод Д.Я. Света [23].
Выражение для сигнала Uλ на выходе приемника излучения тепловизора имеет вид:
 |
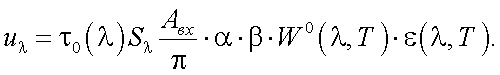(40.1) |
Как видно из (40.1), вычислить T, если ε(λ, T ) – неизвестно, нельзя.
Д.Я. Свет предложил следующую методику построения пирометра (или тепловизора) истинных температур.
Для излучения АЧТ светимость на длине волны λi равна:
 |
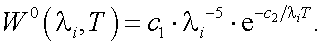(40.2) |
Введем некоторую функцию ω0(λi, T ), которая определяется по формуле:
 |
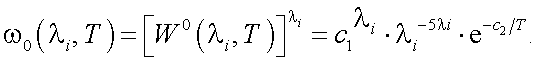(40.3) |
Особенностью функции ω0(λi, T ) является то, что в ней отсутствует смещение max при изменении T. Тогда справедливо соотношение:
 |
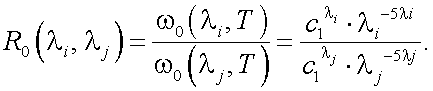(40.4) |
Как видно из соотношения (40.4), функция R0(λi, λj) от T не зависит.
Если имеются реальные тела, то имеем:
 |
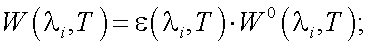(40.5) |
 |
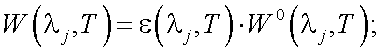(40.6) |
 |
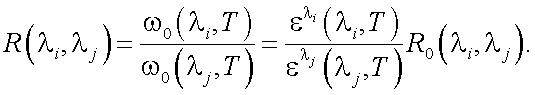(40.7) |
Из (40.7) следует, что если вычислить функцию R(λi, λj) по известным сигналам на эффективных длинах волн λi и λj, то можно найти отношение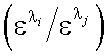 
.
Проделаем это. Сигнал на выходе приемника излучения тепловизора на длине волны λi равен:
 |
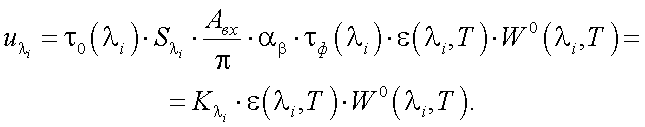(40.8) |
Аналогично, для сигнала на длине волны λj имеем:
 |
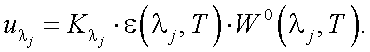(40.9) |
Тогда справедливы соотношения:
 |
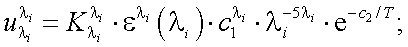(40.10) |
 |
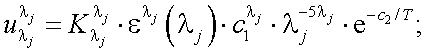(40.11) |
 |
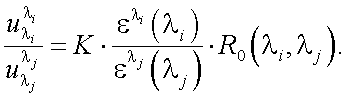(40.12) |
В формуле (40.12) известными величинами являются
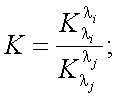
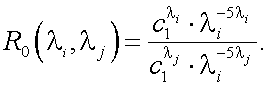
Тогда
 |
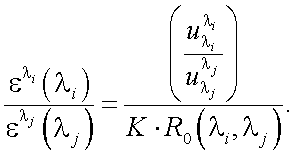(40.13) |
В окончательном виде:
 |
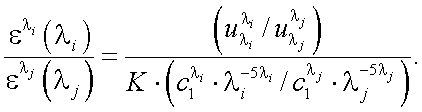(40.14) |
Теперь можно из (40.14) найти ε(λi) и ε(λj).
Решение уравнения (40.14) является очень сложной задачей, но, тем не менее, решение существует. Допустим, что решение найдется в виде:
 |
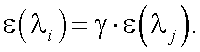(40.15) |
Тогда (40.15) подставим в (40.8):
 |
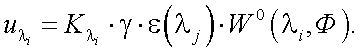(40.16) |
Воспользуемся еще соотношением (40.9):
 |
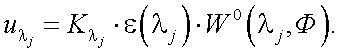(40.17) |
В итоге уравнения (40.16) и (40.17) – это система двух уравнений с неизвестными величинами ε(λj) и T, из которых теперь можно найти истинную температуру T.
Решение проведем следующим образом:
 |
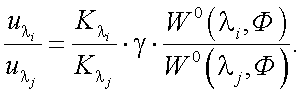(40.18) |
Обозначим через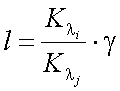 
.
Тогда, на основании (40.18), получим:
 |
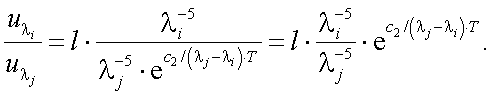(40.19) |
Прологарифмируем (40.19):
 |
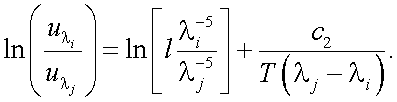(40.20) |
На основании соотношения (40.20) получим следующее уравнение относительно Т:
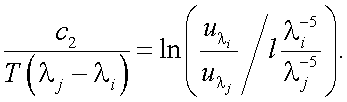
Решение этого уравнения дает следующее значение истинной температуры Т:
 |
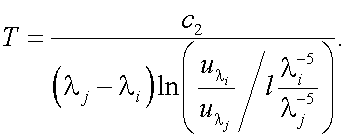(40.21) |
Подставив в (40.21) значение параметра l в развернутом виде выражение для T принимает вид:
 |
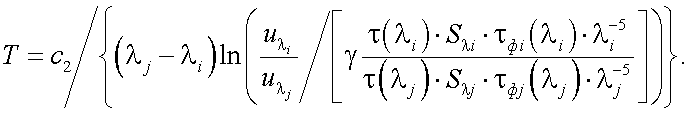(40.22) |
В (40.22) λi, λj – эффективные длины волн измерительного канала тепловизора для двух фильтров с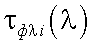 
и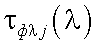 
; при этом λi можно найти по формуле:
 |
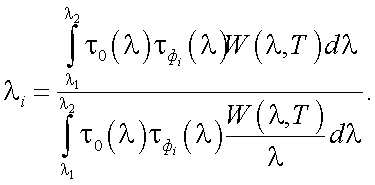(40.23) |
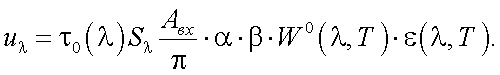
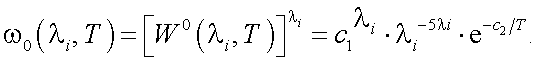
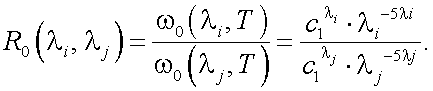
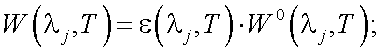
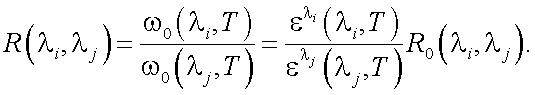
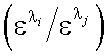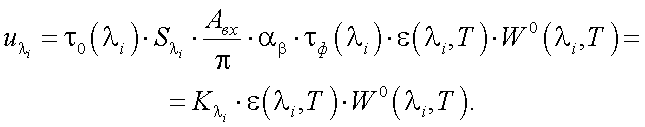
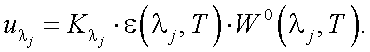
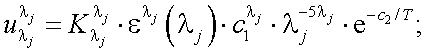
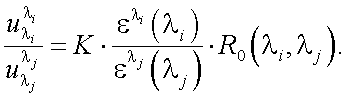
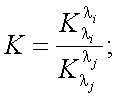
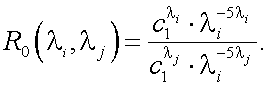
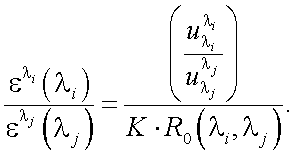
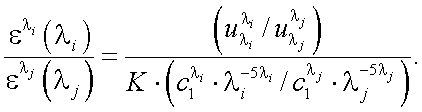
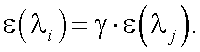
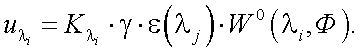
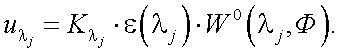
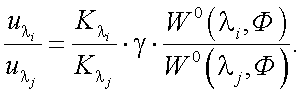
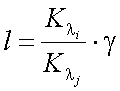