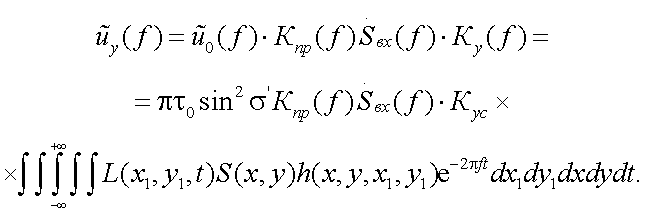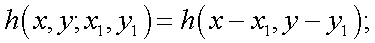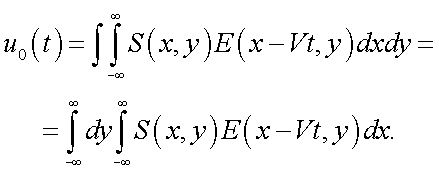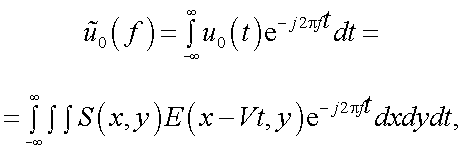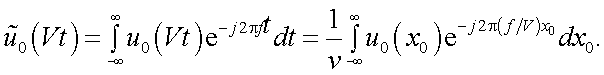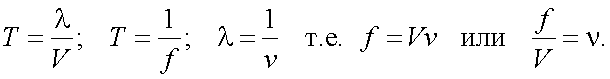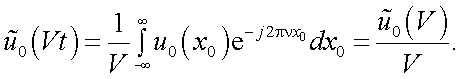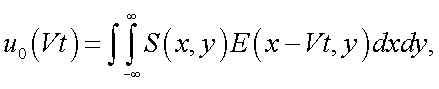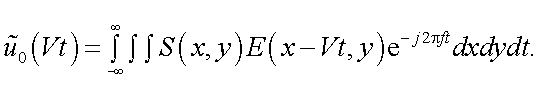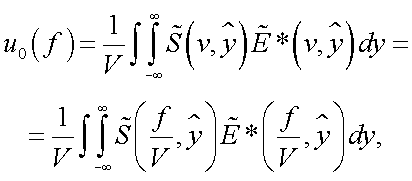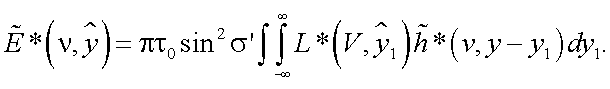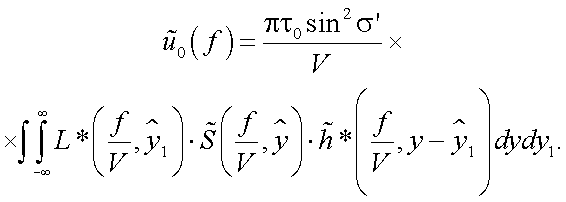Рассмотрим освещенность в изображении применительно к тепловизорам [2]:
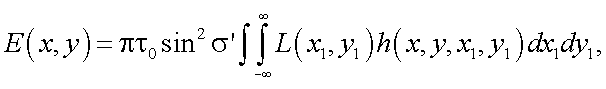 |
(38.1) |
где L(x1, y1) – распределение яркости по поверхности объекта;
h(x, y, x1, y1) – функция рассеяния точки объектива тепловизора;
σ ' – задний апертурный угол объектива тепловизора.
Так как при работе ТПВ ОЭС освещенность E зависит от времени вследствие сканирования по поверхности объекта, то
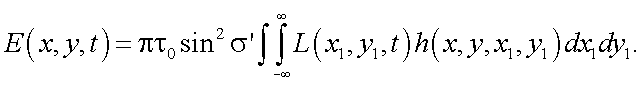 |
(38.2) |
Если в плоскости изображения расположен безынерционный приемник излучения, имеющий распределение чувствительности по координатам х, у – S(x, y), тогда реакция приемника на освещенность E(x, y, t) равна:
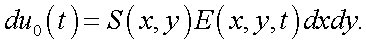 |
(38.3) |
Полная реакция при условии аддитивности реакций, связанных с воздействием потока излучения на элементарные площадки, выражается как
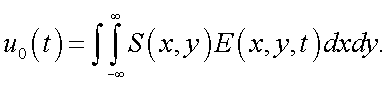 |
(38.3') |
Выражение (38.3 ') определяет форму сигнала, вырабатываемого приемником оптического излучения в ТПВ ОЭС.
Временной спектр этого сигнала будет:
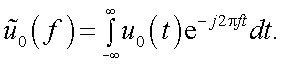 |
(38.4) |
Так как приемник, как правило, инерционный, то спектр сигнала на выходе ПОИ будет:
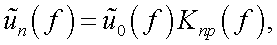 |
(38.5) |
где Kпр( f ) – коэффициент передачи частот приемника излучения.
В свою очередь, спектр сигнала на выходе усилителя равен [2]:
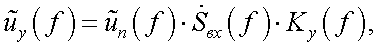 |
(38.5 ') |
где
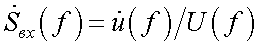 – крутизна входной цепи, состоящей из цепи включения приемника излучения и цепи связи (рис. 38.1).
– крутизна входной цепи, состоящей из цепи включения приемника излучения и цепи связи (рис. 38.1).
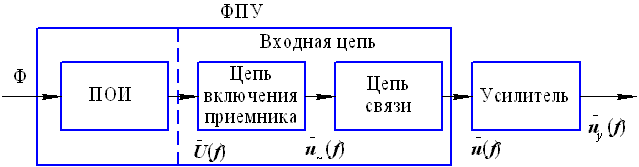
Рис. 38.1. Блок-схема включения приемника излучения и усилителя в тепловизионных ОЭС:
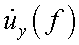 – комплексная амплитуда напряжения сигнала на выходе усилителя;
– комплексная амплитуда напряжения сигнала на выходе усилителя;
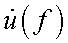 – комплексная амплитуда напряжения сигнала на входе усилителя;
– комплексная амплитуда напряжения сигнала на входе усилителя;
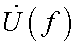 – комплексная амплитуда обобщенного сигнала, вырабатываемого ПОИ;
– комплексная амплитуда обобщенного сигнала, вырабатываемого ПОИ;
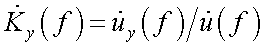 – коэффициент передачи усилителя.
– коэффициент передачи усилителя.
В итоге, спектр сигнала на выходе усилителя равен:
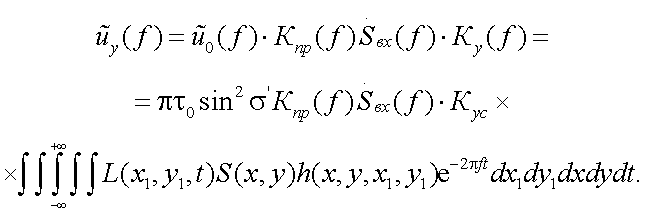 |
(38.6) |
Полученное выражение можно упростить, если ввести допущения:
1) оптическая система обладает свойством изопланарности:
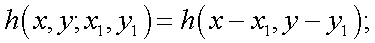
2) задать коэффициент сканирования, тогда зависимость E(x, y, t) от t будет в явном виде.
Если изображение перемещается со скоростью V, и ввести систему координат x'o'y', связанную с подвижным изображением объекта (рис. 38.2), то в этих координатах E(x', y') не зависит от t, а x' = x - Vt, y' = y и E(x', y') = E( x - Vt, y).
Тогда реакция приемника будет:
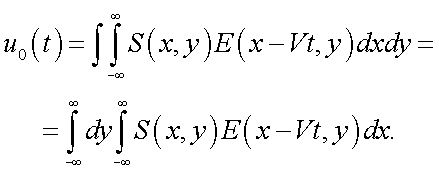 |
(38.7) |
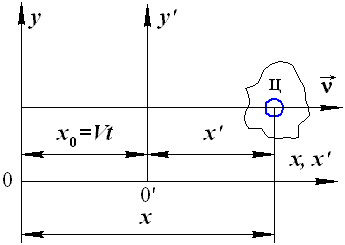
Рис. 38.2. Движение системы координат x’o’y’, связанной с изображением объекта ц
Спектр будет равен:
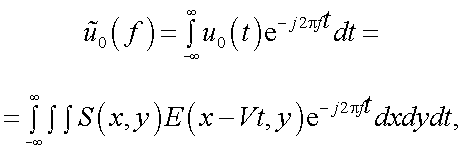
где u0(t) = u0(Vt),
а спектр
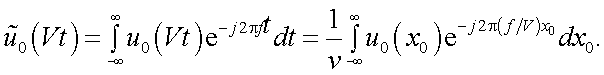
При движении изображения со скоростью V вдоль оси x, пространственный период λ анализируется за время T.
Следовательно:
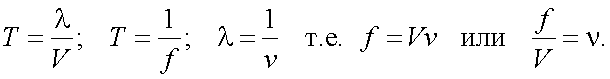
Тогда:
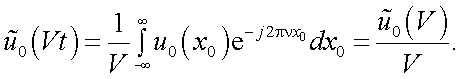 |
(38.8) |
Поскольку
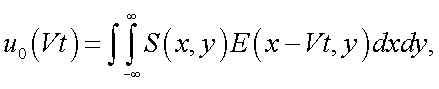
то спектр
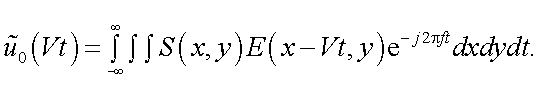
Следовательно:
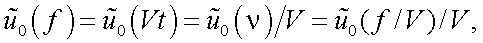 |
(38.9) |
т.е.
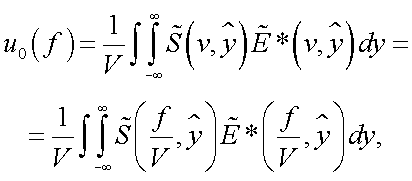 |
(38.10) |
где
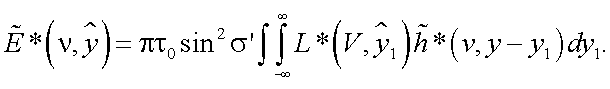 |
(38.11) |
В итоге, подставив (38.11) в (38.10), получим:
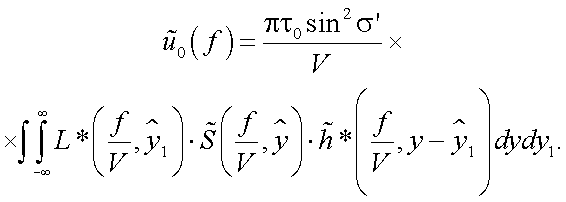 |
(38.12) |

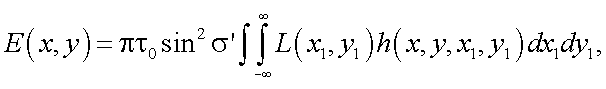
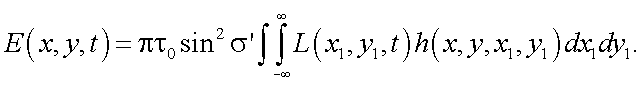
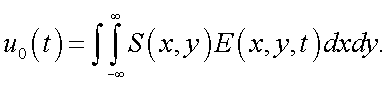
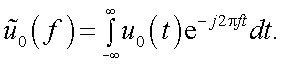
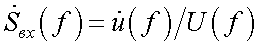 – крутизна входной цепи, состоящей из цепи включения приемника излучения и цепи связи (рис. 38.1).
– крутизна входной цепи, состоящей из цепи включения приемника излучения и цепи связи (рис. 38.1).
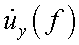 – комплексная амплитуда напряжения сигнала на выходе усилителя;
– комплексная амплитуда напряжения сигнала на выходе усилителя;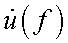 – комплексная амплитуда напряжения сигнала на входе усилителя;
– комплексная амплитуда напряжения сигнала на входе усилителя;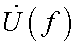 – комплексная амплитуда обобщенного сигнала, вырабатываемого ПОИ;
– комплексная амплитуда обобщенного сигнала, вырабатываемого ПОИ;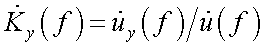 – коэффициент передачи усилителя.
– коэффициент передачи усилителя.