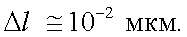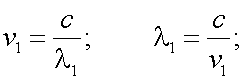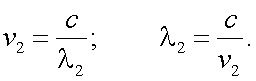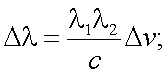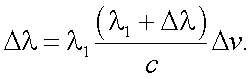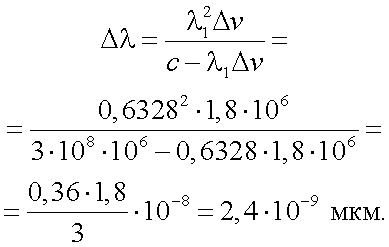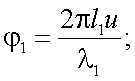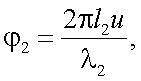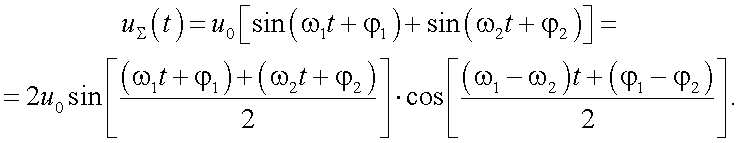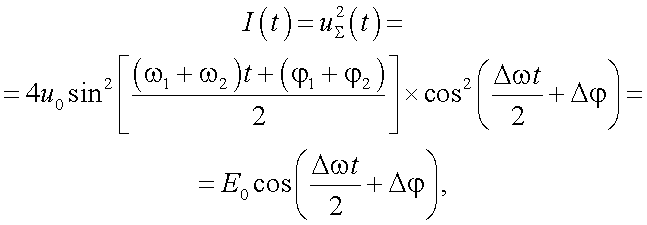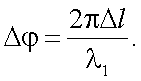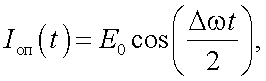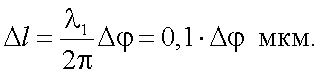Функциональная схема лазерного измерителя перемещений с микропроцессором ИПЛ-МП приведена на рис. 29.1, где приняты следующие обозначения: 1 – лазер; 2 – светоделитель с двоичным покрытием, который пропускает излучение с длиной волны λ1 и отражает излучение с длиной волны λ2; 3, 5 – тетраэдрические отражатели; 4, 7 – плоские зеркала; 6 – полупрозрачное зеркало; 8 – линейный поляризатор; 9 – блок обработки сигналов; 10 – генератор опорных сигналов.
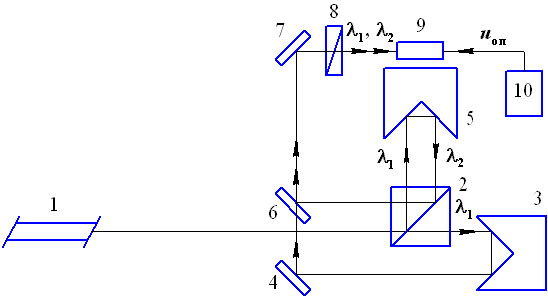
Рис. 29.1. Функциональная схема лазерного измерителя перемещений ИПЛ-МП
Лазерный измеритель перемещений работает следующим образом. Излучение от лазера 1, который генерирует лучи на 2-х близких между собой длинах волн λ1 и λ2, проходит светоделитель 2 с дихроичным покрытием. Лучи, прошедшие дихроичное покрытие, имеют длину волны λ1, а отраженные – длину волны λ2. После светоделителя 2 прошедшие дихроичное покрытие лучи с длиной волны λ1 попадают на тетраэдрический отражатель 3, потом на зеркало 4, проходят полупрозрачное зеркало 6, отражаются от наклонного зеркала 7, проходят линейный поляризатор 8 и попадают в блок обработки сигналов 9, который содержит приемник излучения и микропроцессор. В свою очередь, отраженные дихроичным покрытием лучи с длиной волны λ2 отражаются от тетраэдрического отражателя 5 и диагональной грани светоделителя 2 и направляются на зеркало 6. После отражения от этого зеркала лучи с длиной волны λ2 смешиваются с лучами с длиной волны λ1 и попадают на зеркало 7, проходят линейный поляризатор 8 и попадают в блок обработки сигналов 9.
Обозначим соответствующие сигналы на длинах волн λ1 и λ2, через U1(t) и U2(t), где t – время.
Частоты ν1 и ν2 связаны с соответствующими длинами волн λ1 и λ2 следующими формулами:
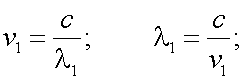 |
(29.1) |
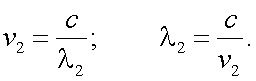 |
(29.2) |
На основании этих формул имеем:
 |
(29.3) |
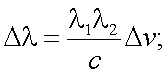 |
(29.4) |
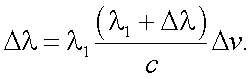 |
(29.5) |
Найдем численные значения изменения длин Δλ по формуле:
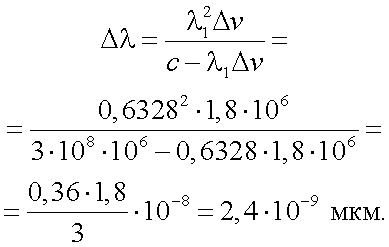 |
(29.6) |
Рассмотрим теперь анализ сигналов и проведем оценку чувствительности измерителя перемещений. Для этого представим сигналы в виде:
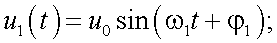 |
(29.7) |
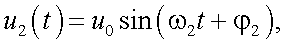 |
(29.7') |
где фазы сигналов имеют вид:
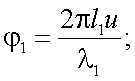 |
(29.8) |
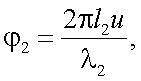 |
(29.8') |
где l1 и l2 – линейные перемещения соответственно призмы 3 и 5;
n – показатель преломления среды, в которой реализуются перемещения.
В приближении скалярных функций суммарный сигнал представим в виде:
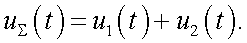 |
(29.9) |
Обозначим энергию суммарного сигнала в виде:
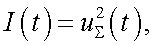 |
(29.10) |
где
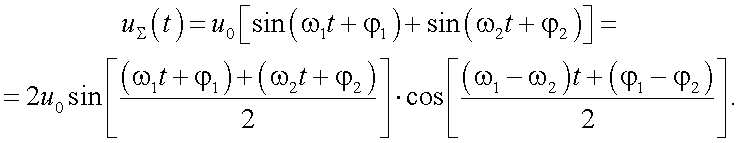 |
(29.11) |
Тогда энергия суммарного сигнала примет вид:
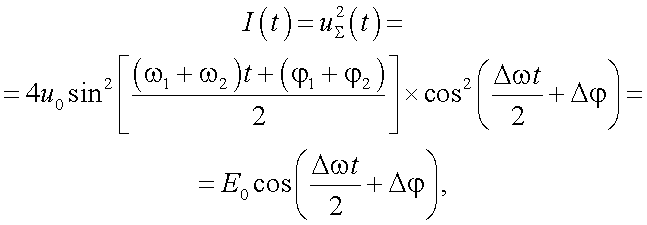 |
(29.12) |
где Е0 – квадрат максимальной амплитуды сигнала;
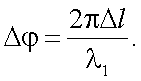 |
(29.13) |
Если из генератора опорных сигналов 10 в блок 9 подать опорное напряжение:
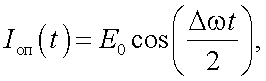 |
(29.14) |
то из разности фаз сигналов минимальное перемещение Δl при λ1 = 0,6328 мкм будет равно:
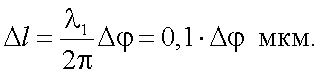
Если Δφ ≈ 0,1 рад, то